A. Fungsi dan Sifatnya
Sebelum membahas beberapa macam fungsi, mari awali bagian ini dengan mengulang pengertian relasi dan fungsi.
1. Pengertian Relasi
Dari himpunan A dan B yang tidak kosong dikatakan bahwa ada suatu relasi
dari A ke B jika ada anggota himpunan A yang berpasangan dengan anggota
himpunan B. Amati diagram pada Gambar 1.
Relasi yang ditunjukkan diagram tersebut dapat dituliskan dalam bentuk himpunan pasangan terurut berikut.
 |
| Gambar 1. Relasi dan anggota himpunan. |
a. {(3, 2), (3, 6), (4, 7), (5, 6)}
b. {(Hasan, Rudi), (Hasan, Ani), (Tina, Rudi)}
c. {(a, x), (b, y), (c, z), (p, q), (r, s)}
Daerah asal (domain) dari relasi pada Gambar 1 (a) adalah {3, 4, 5},
daerah kawannya (kodomain) adalah {2, 6, 7, 8}, dan daerah hasilnya
(range) adalah {2, 6, 7}. Dapatkah Anda menentukan domain, kodomain, dan
range dari Gambar 1 (b) dan (c)?
Misalkan antara x dan y yang keduanya bilangan real terdapat hubungan
(relasi) H, yang dinyatakan sebagai y = 2x. Grafik relasi ini berupa
garis lurus seperti diperlihatkan pada Gambar 2.
Domain relasi ini adalah DH = {x| xϵR}, kodomainnya adalah {y| yϵR} dan rangenya adalah RH = { y| yϵR}.
Titik-titik (x, y) yang memenuhi hubungan ini begitu banyak sehingga
jika dirinci satu per satu tidak mungkin dilakukan. Dalam matematika,
hubungan ini ditulis dengan {(x, y)| y = 2x; x, yϵR}.
 |
| Gambar 2. Grafik relasi. |
Relasi {(x, y)|y = x2 ; x, yϵR} jika disajikan dalam diagram Cartesius terdiri atas semua titik yang terletak pada kurva y = x2 , seperti diperlihatkan pada Gambar 3(a). Adapun relasi {(x, y)|x2 + y2 = 25; x, yϵR} terdiri atas semua titik yang terletak pada x2 + y2 = 25 seperti diperlihatkan pada Gambar 3(b).
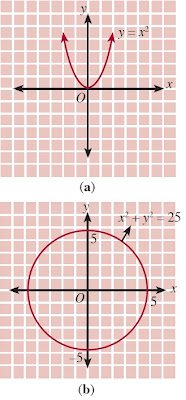 |
| Gambar 3. Grafik relasi (a) fungsi dan (b) bukan fungsi. |
Dari uraian tersebut dapatkah Anda menduga bentuk umum relasi? Cobalah
nyatakan bentuk tersebut dengan kalimat Anda sendiri. Konsep yang telah
Anda pelajari tersebut memperjelas definisi berikut.
Definisi 1
Relasi H dari himpunan A ke himpunan B ialah himpunan bagian dari
himpunan pasangan berurutan yang merupakan himpunan bagian dari A × B.
Jadi, H disebut relasi dari A ke B jika H himpunan bagian dari {(x,
y)|x ϵ A, y ϵ B}.
Domain dari suatu relasi adalah himpunan yang anggotanya terdiri atas unsur-unsur pertama dari semua pasangan berurutan yang merupakan anggota relasi tersebut. Adapun range-nya adalah himpunan yang anggotanya terdiri atas unsur-unsur kedua dari semua pasangan berurutan yang merupakan anggota relasi itu.
2. Pengertian Fungsi
Amati kembali Gambar 2. Pada relasi {(x, y)|y = 2x; x, yϵR}, setiap unsur pada daerah asal (domain) dihubungkan dengan satu dan hanya satu unsur pada daerah hasil (range). Misalnya, –2 dihubungkan dengan –4, –1 dengan –2, 0 dengan 0, 1 dengan 2, 2 dengan 4, dan seterusnya. Sekarang amati Gambar 6.3(a). Pada relasi {(x, y)|y = x2 ; x, yϵR}, setiap unsur pada daerah asal dihubungkan dengan satu dan hanya satu unsur pada daerah hasil; –2 dihubungan dengan 4, –1 dengan 1, 0 dengan 0, 1 dengan 1, 2 dengan 4, dan seterusnya. Relasi {(x, y)|y = 2x; x, yϵR} dan relasi {(x, y)|y = x2 ; x, yϵR} disebut fungsi.
Berbeda dengan Gambar 3 (b), yaitu relasi {(x, y)|x2 + y2 = 25; x, yϵR}. Pada relasi ini, untuk nilai x yang sama misalnya x = 3, terdapat dua nilai y yang berbeda, yaitu y = 4 dan y = –4. Jadi, relasi {(x, y)|x2 + y2 = 25; x, yϵR) bukan fungsi.
Dari uraian tersebut, dapatkah Anda menyatakan pengertian fungsi? Cobalah nyatakan pengertian fungsi dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut memperjelas definisi berikut.
Definisi 2 :
Fungsi ialah relasi dengan setiap unsur dari daerah asalnya dipasangkan dengan tepat satu unsur dari daerah kawannya.
Contoh Soal 1 :
Di antara grafik pada Gambar 4, manakah yang menyatakan suatu fungsi dari R → R, x, yϵR? Jelaskan jawaban Anda.
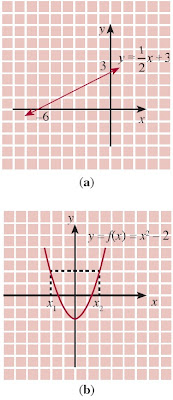 |
| Gambar 4. Grafik (a) bukan merupakan fungsi (b) menyatakan fungsi. |
Penyelesaian :
a. Dari Gambar 4(a) tampak bahwa untuk x = 3 dihubungkan dengan yϵR, misalnya 3 dengan 0, 3 dengan 1, 3 dengan 2, dan seterusnya. Akibatnya, relasi {(x,y)| x = 3; x, yϵR} bukan merupakan fungsi.
b. Dari Gambar 4(b) tampak bahwa setiap unsur pada domain dihubungkan
dengan satu dan hanya satu unsur pada range. Misalnya, 4 dihubungkan
dengan 2; –2 dihubungkan dengan –1; 0 dihubungkan dengan 0; 2 dengan 1;
dan seterusnya. Dengan demikian, relasi {(x,y)| y = 1/2 x; x, yϵR} merupakan fungsi. Grafik pada Gambar 4(b), menyatakan fungsi.
Contoh Soal 2 :
Diketahui fungsi f : R → R dan f(x) = x2 – 1.
a. Hitunglah f(–3), f(–1), f(0), f(2), dan f(3).
b. Jika f(a) = 3, tentukan nilai a yang memenuhi.
c. Gambarkan grafik fungsi tersebut.
d. Jika daerah asal fungsi tersebut adalah D f = { x|–3 ≤ x ≤ 3, xϵR}, tentukan daerah hasilnya.
Pembahasan :
a. f(x) = x2 – 1
f(–3) = (–3)2 – 1 = 9 – 1 = 8
f(–1) = (–1)2 – 1 = 0
f(0) = (0)2 – 1 = –1
f(2) = (2)2 – 1 = 3
f(3) = (3)2 – 1 = 8
b. f(a) = a2 – 1
3 = a2 – 1
a2 = 3 + 1
a2 = 4
a2 = 4
a =
±2Jadi, nilai a yang memenuhi adalah a = 2 dan a = –2.
d. Daerah hasil dari fungsi y = f(x) = x2 – 1 adalah Rf = { y| –1 ≤ y ≤ 8, yϵR}
3. Sifat-Sifat Fungsi
a. Fungsi Injektif
Misalkan, himpunan A = {1, 2, 3} dan himpunan B = {p, q, r, s}. Dari himpunan A ke himpunan B ditentukan fungsi f dan fungsi g yang dinyatakan dengan diagram panah pada Gambar 6.
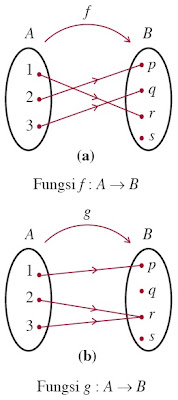 |
| Gambar 6. Diagram panah fungsi injektif atau fungsi satu-satu. |
Pada Gambar 6(a), untuk setiap anggota himpunan A yang berbeda mempunyai
peta yang berbeda di himpunan B. Fungsi yang demikian dinamakan fungsi
injektif atau fungsi satu-satu.
Pada Gambar 6(b), terdapat dua anggota himpunan A yang berbeda, yaitu 2
dan 3 mempunyai peta yang sama, yaitu r di himpunan B. Oleh karena itu,
fungsi g bukan fungsi injektif.
Sekarang, amati kembali Gambar 2. Dari grafik fungsi f(x) = 2x pada gambar tersebut, untuk setiap domain x1 dan x2 (x1 ≠ x2) maka f(x1) ≠ f(x2). Misalkan untuk x1 = –1, x2 = 1 maka f(x1) = –2, f(x2) = 2, dan f(x1) ≠ f(x2). Jadi, untuk nilai x yang berbeda menghasilkan nilai y = f(x) yang berbeda pula. Fungsi yang demikian disebut fungsi injektif atau fungsi satu-satu.
Amati pula grafik fungsi f(x) = x2 pada Gambar 3(a).
Pada fungsi ini, untuk setiap domain x1 dan x2 (x1 ≠ x2) terdapat hubungan f(x1) = f(x2), misalnya f(–1) = f(1) = 1 dan f(–2) = f(2) = 4. Jadi, untuk nilai x yang berbeda terdapat nilai y = f(x) yang sama. Fungsi yang demikian bukan merupakan fungsi injektif.
Secara umum, jika f fungsi dari himpunan A ke himpunan B maka setiap unsur di dalam A dikawankan dengan tepat suatu unsur tertentu yang khas di dalam B. Jika dua unsur yang berbeda di dalam A masing-masing dikawankan dengan tepat satu unsur yang berbeda pula di dalam B maka f disebut fungsi injektif atau fungsi satu-satu.
b. Fungsi Surjektif
Misalkan, himpunan A = {1, 2, 3} dan himpunan B= {x, y, z}. Dari himpunan A ke himpunan B ditentukan fungsi f yang ditentukan dengan diagram panah pada Gambar 7(a).
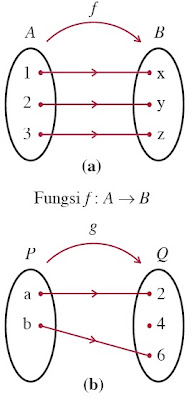 |
| Gambar 7. Diagram panah Fungsi Surjektif. |
Jadi, fungsi f pada Gambar 7(a) merupakan fungsi surjektif.
Coba Anda selidiki Gambar 7(b). Apakah fungsi g : P → Q merupakan fungsi surjektif? Jelaskan jawaban Anda. Sekarang, amatilah grafik f(x) = 2x (Gambar 2). Grafik tersebut memiliki daerah hasil (range) Rf sama dengan daerah kawannya (kodomainnya). Oleh karena itu, fungsi f(x) = 2x disebut fungsi surjektif atau fungsi onto. Secara umum, jika pada suatu fungsi f dari A ke B daerah hasilnya Rf = B maka fungsi itu disebut fungsi surjektif atau fungsi onto.
Akan tetapi, jika Rf ⊂ B maka fungsi tersebut bukan merupakan fungsi surjektif. Suatu fungsi yang bersifat injektif dan surjektif disebut fungsi bijektif. Jadi, fungsi y = 2x merupakan fungsi bijektif.
Contoh Soal 3 :
Selidikilah fungsi berikut, apakah merupakan fungsi injektif atau bukan, jika injektif apakah juga merupakan fungsi bijektif?
a. y = f(x) = 1/2 x + 3, xϵR,
b. y = f(x) = x2 – 2, xϵR,
Kunci Jawaban :
a. Grafik fungsi y = f(x) = 1/2 x + 3, x ϵ R tampak pada Gambar 8 (a).
 |
| Gambar 8. Grafik (a) fungsi bijektif (b) bukan fungsi injektif. |
b. Grafik dari fungsi y = f(x) = x2 – 2, xϵR diperlihatkan pada Gambar 8(b). Pada gambar tersebut, tampak bahwa terdapat nilai-nilai x1 , x2 ϵ Df dengan x1 ≠ x2 , tetapi f(x1) = f(x2). Jadi, fungsi y = f(x) = x2 – 2, xϵR bukan fungsi injektif.
B. Aljabar Fungsi
Anda telah mempelajari fungsi si f(x) = x2 – 2 mempunyai daerah asal Df = { x| xϵR}. Demikian halnya dengan fungsi g(x) =
• (f + g)(x) = f(x) + g(x) = x2 – 2 +
(f – g)(x) = f(x) – g(x) = x2 – 2 – 
• (f . g)(x) = f(x) . g(x) = (x2 – 2) 
Anda pun akan mempelajari cara menentukan daerah asal fungsi hasil
operasi. Untuk itu pelajari uraian berikut. Misalkan, f(x) dan g(x)
adalah fungsi-fungsi yang diketahui, berlaku hal-hal berikut.
• Jumlah dari fungsi f(x) dan g(x) adalah :
(f + g)(x) = f(x) + g(x) dengan Df + g = Df ∩ Dg
• Selisih dari fungsi f(x) dan g(x) adalah :
(f – g)(x) = f(x) – g(x) dengan Df - g = Df ∩ Dg
• Perkalian dari fungsi f(x) dan g(x) adalah :
(f × g)(x) = f(x) × g(x) dengan Df x g = Df ∩ Dg
• Pembagian dari fungsi f(x) dan g(x) adalah :
Contoh Soal 4 :
Diketahui fungsi f(x) = x2 – 5 dan g(x) = 2 , tentukan operasi fungsi-fungsi berikut. Tentukan pula daerah asalnya.
, tentukan operasi fungsi-fungsi berikut. Tentukan pula daerah asalnya.
a. (f + g) (x)
b. (f – g) (x)
c. (f × g) (x)
d. (f/g) (x)
Pembahasan :
Df = {x | xϵR} dan Dg ={x | x ≥ 0, xϵR}.
a. (f + g)(x) = f(x) + g(x) = x2 – 5 + 2
Df + g = Df ∩ Dg = {x | xϵR} ∩{x | x ≥ 0, xϵR}
= {x | x ≥ 0, xϵR}
b. (f – g) (x) = f(x) – g(x) = x2 – 5 – 2
Df - g = {x | x ≥ 0, xϵR}
c. (f - g)(x) = f (x) - g(x) 2x2  - 10
- 10
Df x g = {x | x ≥ 0, xϵR}
d. 
Df/s = {x | x > 0, x R}
C. Fungsi Komposisi
1. Pengertian Fungsi Komposisi
Sebelum Anda mempelajari fungsi komposisi lebih lanjut, pelajari uraian berikut ini. Misalkan f(x) = x2 + 1 dengan Df = { x| xϵR} dan g(x) =
 |
| Gambar 9. fungsi komposisi g°f adalah pemetaan xϵDf oleh fungsi f, kemudian bayangannya dipetakan lagi oleh g. |
Mula-mula unsur xϵDf dipetakan
oleh f ke bayangan x, yaitu f(x). Kemudian, f(x) dipetakan oleh g ke
g(f(x)). Dengan demikian, fungsi komposisi g°f adalah pemetaan xϵDf oleh fungsi f, kemudian bayangannya dipetakan lagi oleh g. Uraian tersebut memperjelas definisi berikut.
Definisi 3 :
Diketahui, f dan g dua fungsi sebarang maka fungsi komposisi f dan g
ditulis g ° f, didefinisikan sebagai (g ° f)(x) = g(f(x)) untuk setiap xϵDg .
Untuk x = 1 Anda peroleh f(x) = 2 yang berada dalam daerah asal fungsi
g. Bayangan x, yaitu f(x) = 2 dapat dipetakan oleh g ke g(f(x)) sebab
g(2) =  = 0
= 0
Lain halnya jika x = 1/2. Untuk x = 1/2 diperoleh f(x) = 1 1/4 yang
berada di luar daerah asal fungsi g. Bayangan x, yaitu f(x) = 1 1/4
tidak dapat dipetakan oleh g ke fungsi komposisi g(f(x)) sebab  nilai
ini tidak terdefinisi jika Anda membatasi daerah kerja pada himpunan
seluruh bilangan real. Dari uraian itu dapat dipahami bahwa pemetaan
berantai baru dapat dilakukan jika bayangan x jatuh ke dalam daerah asal
fungsi g. Dengan demikian, diperoleh daerah asal fungsi komposisi g ° f
adalah :
nilai
ini tidak terdefinisi jika Anda membatasi daerah kerja pada himpunan
seluruh bilangan real. Dari uraian itu dapat dipahami bahwa pemetaan
berantai baru dapat dilakukan jika bayangan x jatuh ke dalam daerah asal
fungsi g. Dengan demikian, diperoleh daerah asal fungsi komposisi g ° f
adalah :
D gof = {x | x ϵ Df , f (x) ϵ Dg}.
Dengan pemikiran yang sama, fungsi komposisi f ° g adalah pemetaan xϵDg oleh fungsi g, kemudian bayangannya dipetakan lagi oleh f. Dengan demikian, daerah asal fungsi komposisi f ° g adalah :
D fog = {x | x ϵ Dg , f (x) ϵ Df}.
Misalkan diketahui f(x) = x2 + 2 dan g(x) =  . Kedua fungsi itu dapat digambarkan seperti Gambar 10.
. Kedua fungsi itu dapat digambarkan seperti Gambar 10.
 |
| Gambar 10. f(x) yang berada di luar daerah asal fungsi g. Bayangan x, yaitu f(x) tidak dapat dipetakan oleh g ke fungsi komposisi g(f(x)). |
Daerah hasil R f = { x| x ≥ 2, xϵR} tidak dapat dipetakan oleh g(x) =  sebab untuk x ≥ 2, g(x) tidak terdefinisi.
sebab untuk x ≥ 2, g(x) tidak terdefinisi.
Coba jelaskan mengapa g(x) tidak terdefinisi untuk x ≥ 2. Jika Anda analisis uraian tersebut, diperoleh hal-hal berikut.
Coba jelaskan mengapa g(x) tidak terdefinisi untuk x ≥ 2. Jika Anda analisis uraian tersebut, diperoleh hal-hal berikut.
• Fungsi f(x) = x2 + 1 dan g(x) =
Rf ∩ Dg = { x| x ≥ 1, xϵR} ∩ {x| x ≥ 2, xϵR} = {x| x ≥ 2, xϵR}.
• Fungsi f(x) = x2 + 2 dan g(x) =  tidak
dapat dikomposisikan menjadi fungsi komposisi g ° f sebab irisan antara
daerah hasil fungsi f dan daerah asal fungsi g merupakan himpunan
kosong.
tidak
dapat dikomposisikan menjadi fungsi komposisi g ° f sebab irisan antara
daerah hasil fungsi f dan daerah asal fungsi g merupakan himpunan
kosong.
Rf ∩ Dg = {x| x ≥ 2, xϵR} ∩ {x| x ≤ 1, xϵR} = Ø.
Syarat yang harus dipenuhi agar fungsi f dan fungsi g dapat
dikomposisikan menjadi fungsi komposisi (g ° f) adalah irisan antara
daerah hasil fungsi f dan daerah asal fungsi g bukan himpunan kosong,
atau Rf ∩ Dg ≠ Ø.
Contoh Soal 5 : Soal Ebtanas 1999
Fungsi g: R → R ditentukan oleh g(x) = x2 – x + 3 dan fungsi f: R → R sehingga (f ° g)(x) = 3x2 – 3x + 4 maka f (x – 2) = ....
Penyelesaian :
g(x) = x2 – x + 3
(f ° g) (x) = 3x2 – 3x + 4
f(g(x)) = 3(x2 – x + 3) – 5
f (x) = 3x – 5
maka f(x – 2) = 3(x – 2) – 5
= 3x – 11
Contoh Soal 6 :
a. Jika f(x) = 2x3 dan g(x) = x + 3, tentukan g ° f(x).
b. Jika g(x) = 2x + 4 dan h(x) = x2 + 2x +5, tentukan h ° g(x).
Jawaban :
a. g ° f(x) = g {f (x)} = f(x) + 3 = 2x3 + 3
b. h ° g(x) = h{g(x)} = {g(x)}2 + 2{g(x)} + 5
= (2x + 4)2 + 2(2x + 4) + 5
= 4x2 + 16x + 16 + 4x + 8 + 5
=
4x2 + 20x + 29
Contoh Soal 7 :
Diketahui f(x) = 2x + 5 dan g(x) = 3x2 . Tentukan:
a. (f ° g) (x) dan (g ° f) (x)
b. 1. daerah asal (f ° g) (x) dan daerah hasil (f ° g) (x)
2. daerah asal (g ° f) (x) dan daerah hasil (g ° f) (x)
Pembahasan :
a. (f ° g) (x) = f (g (x)) = f (3x2) = 2(3x2) + 5 = 6x² + 5
(g ° f) (x) = g (f (x)) = g (2x + 5) = 3 (2x + 5)2
= 3(4x2 + 20x + 25) = 12x2 + 60x + 75
b. 1. Daerah asal (f ° g) (x) = D
f ° g = {x|xϵR} dan daerah hasil (f ° g) (x) = R
f ° g = {y|yϵR}.
2. Daerah asal (g ° f) (x) = Dg°f = {x|xϵR} dan daerah hasil (g ° f) (x) = Rg°f = {y|yϵR}.
2. Sifat-Sifat Komposisi Fungsi
Untuk mempelajari sifat-sifat komposisi fungsi, pelajari uraian berikut. Diketahui, f(x) = x + 5 dan g(x) = 2x + 6.
(f ° g) (x) = f (g(x)) = f (2x + 6) = (2x + 6) + 5 = 2x + 11
(g ° f) (x) = g (f (x)) = g (x + 5) = 2(x + 5) + 6 = 2x + 16
Amati lagi hasil contoh 6.5. Apakah nilai (f ° g)(x) sama dengan (g ° f) (x)? Coba selidiki untuk fungsi lainnya. Apa yang Anda peroleh? Jika melakukannya dengan benar, akan diperoleh kesimpulan berikut.
(f ° g) (x) ≠ (g ° f) (x)
Amati fungsi f(x) = 2x + 1, g(x) = x2 , dan h(x) = 3x + 5.
Misalkan, (g ° h) (x) = s(x) maka :
s(x) = (g ° h) (x) = g (h (x)) = g (3x + 5) = (3x + 5)2 = 9x2 + 30x + 25
sehingga :
(f ° (g ° h))(x) = (f ° s) (x) = f(s(x)) = f (9x2 + 30x + 25)
= 2(9x2 + 30x + 25) + 1 = 18x2 + 60x + 50 + 1
= 18x2 + 60x + 51
Jadi, (f ° g ° h) (x) = 18x2 + 60x + 51.
Kemudian, misalkan (f ° g) (x) = t(x) maka :
t(x) = (f ° g) (x) = f (g (x)) = f (x2) = 2x2 + 1 sehingga :
((f ° g) ° h) (x) = (t ° h) (x) = t(h(x)) = t (3x + 5)
= 2(3x + 5)2 + 1
= 2(9x2 + 30x + 25) + 1 = 18x2 + 60x + 51
Jadi, (f ° (g ° h)) (x) = 18x2 + 60x + 51.
Amati lagi uraian tersebut. Apa yang Anda peroleh mengenai nilai f ° (g ° h)(x) jika dihubungkan dengan nilai (f ° g) ° h(x)? Apakah hal ini berlaku untuk fungsi yang lainnya? Untuk itu, bersama dengan teman sebangku buat 3 buah fungsi. Kemudian, hitung nilai f ° (g ° h) dan (f ° g) ° h. Apakah hasil keduanya sama? Ulangi lagi untuk fungsi lainnya. Apakah Anda dapat memperoleh kesimpulan berikut?
(f ° (g ° h)) (x) = ((f ° g) ° h) (x)
Contoh Soal 9 :
Diketahui f(x) = 5x2 + 6 dan I(x) = x.
a. Carilah (f ° I)(x) dan (I ° f) (x).
b. Apakah (f ° I)(x) = (I ° f) (x)?
Pembahasan :
a. (f ° I)(x) = f (I (x)) = f(x) = 5x2 + 6
(I ° f)(x) = I (f (x)) = I (5x2 + 6) = 5x2 + 6
b. Dari hasil (a) tampak bahwa (f ° I)(x) = (I ° f) (x).
Dalam hal ini fungsi I(x) = x disebut fungsi identitas terhadap operasi komposisi fungsi.
Dari uraian tersebut, dapatkah Anda menduga sifat-sifat komposisi
fungsi? Cobalah nyatakan sifat-sifat komponen fungsi dengan kata-kata
Anda sendiri.
• Operasi komposisi pada fungsi-fungsi pada umumnya tidak komutatif.
(f ° g)(x) ≠ (g ° f)(x)
• Operasi komposisi pada fungsi-fungsi bersifat asosiatif
(f ° (g ° h))(x) = ((f ° g) ° h)(x)
• Dalam operasi komposisi pada fungsi-fungsi terdapat sebuah fungsi identitas, yaitu I(x) = x sehingga (f ° I)(x) = (I ° f)(x) = f(x)
3. Menentukan Fungsi f atau g jika Diketahui Fungsi Komposisi dari f atau g
Pada bagian sebelumnya, Anda telah belajar menentukan fungsi komposisi f
° g atau g ° f jika fungsi f dan g diketahui. Bagaimana jika terjadi
sebaliknya? Fungsi yang diketahui adalah fungsi komposisi dan salah satu
fungsi yang membentuk komposisi fungsi tadi, bagaimana cara menentukan
fungsi lainnya?
Anda dapat menentukan fungsi g(x) jika diketahui fungsi komposisi (f ° g) (x) = 10x – 5 dan f(x) = 2x – 5, yaitu sebagai berikut.
(f ° g)(x) = 10x – 5
f(g(x)) = 10x – 5
2(g(x)) – 5 = 10x – 5
2 (g(x)) = 10x
g(x) = 5x
Untuk ntuk menentukan fungsi f(x) jika diketahui fungsi komposisi (f ° g)(x) = 30x2 – 15 dan g(x) = 10x2 – 3 caranya sebagai berikut.
(f ° g)(x) = 30x2 – 15
f(g(x)) = 30x2 – 15
f(10x2 – 3) = 30x2 – 15 = 3(10x2 – 3) – 15 + 9
f(10x2 – 3) = 3(10x2 – 3) – 6
f(x) = 3x – 6
Jika fungsi f dan fungsi komposisi f ° g atau g ° f diketahui maka fungsi g dapat ditentukan. Demikian juga jika fungsi g dan fungsi komposisi f ° g atau g ° f diketahui maka fungsi f dapat ditentukan.
Contoh Soal 10 :
Diketahui f ° g (x) = 1/x dan f (x) =  Tentukan g(x).
Tentukan g(x).
Jawaban :
f ° g (x) = 1/x f (g (x)) = 1/x
↔ x = g 
↔ g(x) = x2
Di SMP, tentunya Anda telah belajar cara mengubah satuan dari derajat Celsius ke Fahrenheit, yaitu dengan menggunakan persamaan y = 9/5 x + 35. Bagaimana cara mengubah satuan dari Fahrenheit ke Celsius? Untuk mengetahuinya, Anda harus belajar fungsi invers. Apakah setiap fungsi selalu memiliki fungsi invers? untuk mengetahuinya, lakukan aktivitas matematika berikut.
Aktivitas Matematika
Lakukanlah kegiatan berikut bersama kelompok Anda.
Langkah ke-1
a. Melengkapi tabel fungsi y = f(x)
Misalkan fungsi si f dari x ke y didefinisikan sebagai y= f(x), seperti Tabel 1. Salin dan lengkapilah Tabel 1. di buku tugas Anda.
Tabel 1. Fungsi y = f(x)
x (masukan)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
y (keluaran)
|
0
|
2
|
4
|
6
|
8
|
...
|
...
|
...
|
...
|
b. Menukarkan nilai-nilai masukan dan keluaran
Tukarkan nilai-nilai masukan dan keluaran tersebut seperti Tabel 2, kemudian salin dan lengkapilah Tabel 2. di buku tugas Anda.
Tabel 2.
x (masukan)
|
0
|
2
|
4
|
6
|
8
|
...
|
...
|
...
|
...
|
y (keluaran)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Coba Anda selidiki, apakah Tabel 2. merupakan fungsi dari y ke x?
Tuliskan hasil penyelidikan Anda di buku tugas Anda. Langkah ke-2
a. Melengkapi tabel fungsi s = g(r)
Misalkan fungsi g dari r ke s didefinisikan sebagai s = g(r), seperti Tabel 3. Salin dan lengkapilah Tabel 3. di buku tugas Anda.
Tabel 3. Fungsi s = g(r)
x (masukan)
|
-4
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
y (keluaran)
|
...
|
9
|
4
|
1
|
0
|
1
|
4
|
9
|
...
|
b. Menukarkan nilai-nilai masukan dan keluaran
Tukarkan nilai-nilai masukan dan keluaran tersebut seperti Tabel 6.2, lalu salin dan lengkapi Tabel 6.4 di buku tugas Anda.
Tabel 4.
x (masukan)
|
...
|
9
|
4
|
1
|
0
|
1
|
4
|
9
|
...
|
y (keluaran)
|
–4
|
–3
|
–2
|
–1
|
0
|
1
|
2
|
3
|
4
|
Coba Anda selidiki, apakah Tabel 4. merupakan fungsi dari s ke r?
Tuliskan hasil penyelidikan Anda di buku tugas Anda.
Langkah ke-3
Dapatkah Anda menduga, fungsi yang bagaimana yang memiliki fungsi invers? Jawablah dengan cara menganalisis Tabel 1. sampai dengan Tabel 4.
Ingatlah :
Lambang –1 di dalam f–1 bukan berupa pangkat.
Jika fungsi f memetakan setiap xϵDf ke yϵRf maka
balikan dari fungsi f mengembalikan unsur y tersebut ke unsur x semula.
Proses pembalikan tersebut belum tentu menghasilkan fungsi baru. Jika f
fungsi bijektif maka pembalikan tersebut menghasilkan fungsi baru. Akan
tetapi, jika f bukan fungsi bijektif pembalikan itu hanya menghasilkan
suatu relasi. Agar lebih jelas, pelajari uraian berikut. Telah diketahui
fungsi y = 2x seperti Gambar 12 merupakan fungsi bijektif.
 |
| Gambar 12. Fungsi bijektif. |
Amati bahwa setiap dua unsur yang berbeda di dalam domain f dikawankan
dengan dua unsur yang berbeda di dalam daerah kawan f. Sebagai contoh, x1 = 2 dan x2 = –2 dikawankan berturut-turut dengan y1 = 4 dan y2 =
–4. Balikan dari fungsi ini akan menghubungkan dua unsur yang berbeda
tersebut dengan dua unsur semula yang berbeda, yaitu 4 dengan 2 dan –4
dengan –2.
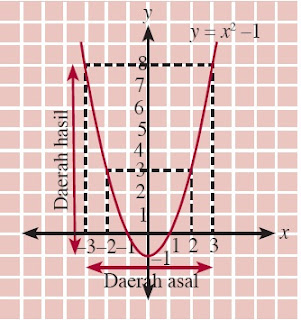
Balikan dari fungsi tersebut jelas sesuai dengan aturan fungsi, yang hanya membolehkan setiap unsur di dalam daerah asalnya dihubungkan dengan satu dan hanya satu unsur di dalam daerah hasil. Jadi, balikan dari fungsi f(x) = 2x merupakan fungsi. Lain halnya dengan fungsi y = x2 seperti Gambar 13. Fungsi ini bukan merupakan fungsi bijektif.
 |
| Gambar 13. Bukan fungsi bijektif. |
Amati bahwa setiap unsur x dan –x di dalam domain f dikawankan dengan
unsur y yang sama di dalam daerah kawan f. Contohnya, unsur 2 dan –2
keduanya dipetakan ke unsur yang sama, yaitu 4. Akibatnya, balikan dari
fungsi ini menghubungkan 4 dengan dua unsur yang berbeda, yaitu 2 dan
–2. Balikan dari fungsi ini jelas menyalahi aturan fungsi.
Jadi, balikan dari fungsi f(x) = x2 bukan merupakan fungsi, tetapi hanya relasi saja.
Dari uraian tersebut dapatkah Anda menduga bentuk umum fungsi invers? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut memperjelas definisi berikut.
Definisi 4 :
Misalkan, f merupakan fungsi bijektif dengan daerah asal Df dan daerah hasil Rf R.. Fungsi invers(fungsi balikan) f adalah f–1 jika dan hanya jika (f–1 ° f) (x) = x untuk setiap x di dalam D f dan (f–1 ° f) (x) = x untuk setiap x di dalam R f
Dari Definisi 6.4 tampak bahwa setiap xϵD f dipetakan oleh f ke f(x) dan f(x) oleh f–1 dikembalikan ke x. Demikian halnya untuk setiap xϵR f dipetakan oleh f–1 ke f–1(x) dan f–1 x) oleh f dikembalikan ke x. Dengan demikian, invers suatu fungsi invers menghasilkan fungsi asalnya, dituliskan (f–1)–1 = f. Dari uraian tersebut, Anda dapat menentukan invers suatu fungsi dengan langkah-langkah sebagai berikut.
• Diketahui, y = f(x).
• Selesaikan persamaan sehingga diperoleh x sebagai fungsi y atau x = f–1(y).
• Ganti variabel y dengan x pada f–1(y) sehingga diperoleh f–1(x) = y sebagai fungsi invers dari y = f(x).
Contoh Soal 11 :
Tentukan invers dari fungsi berikut ini.
y = f (x) = 5x – 7
Kemudian, gambarkan grafik f (x) dan f–1 (x).
Penyelesaian :
y = 5x – 7 ↔ 5x = y + 7
x = 
x = f-1 (y) = 
Jadi, fungsi invers dari y = f (x) = 5x – 7 adalah f –1 (x) =  . Gambar grafik f (x) = 5x – 7 dan f–1 (x) =
. Gambar grafik f (x) = 5x – 7 dan f–1 (x) =  tampak pada Gambar 14.
tampak pada Gambar 14.
Amati Gambar 14. dengan saksama, bagaimana posisi grafik f(x) dan f–1(x) terhadap y = x. Apakah simetris?
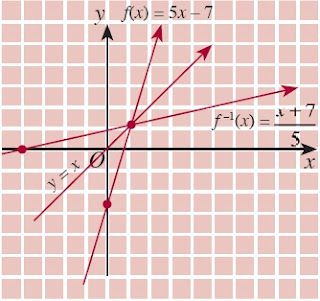 |
| Gambar 14. Fungsi invers. |
Jika Anda amati grafik f (x) dan f–1 x) dengan saksama, tampak bahwa grafik f–1 x) simetris terhadap grafik f(x). Grafik f–1 x) diperoleh dari grafik f(x) dengan mencerminkannya terhadap garis y = x. Oleh karena itu, untuk mencari f–1 x) jika diketahui f (x) dapat pula dikerjakan dari persamaan f ° f–1 x) = x. Coba Anda selesaikan invers dari f(x) = 5x – 7 dengan menggunakan f ° f–1(x) = x.
Contoh Soal 12 :
1. Diketahui f (x) = 3x2 + 4 dan 
Periksalah apakah g merupakan balikan (invers) dari f.
2. Tentukan fungsi invers dari
Pembahasan :
1. Untuk menentukan apakah g fungsi invers f, periksalah apakah fungsi komposisi (g ° f) (x) = x dan (f ° g) (x) = x.(g ° f) (x) = g {f (x)} = g (3x2 + 4) =
(f ° g) (x) = f {g (x)} = 

= x – 4 + 4 = x
Jadi, g merupakan balikan f sehingga f juga balikan g. Dengan kata lain, g = f–1 dan f = g–1 .
2. y = f (x) =  ↔ y (2x–1) = 3x + 4
↔ y (2x–1) = 3x + 4
↔ 2yx – y = 3x + 4
↔ x (2y – 3) = y + 4
↔ 2yx – 3x = y + 4
↔ 2yx – 3x = y + 4
↔ x = 
↔ x = f–1 (y) = 
Jadi, f–1 (x) =
E. Invers dari Fungsi Komposisi
Seperti halnya fungsi yang lain, fungsi komposisi dapat memiliki invers, asalkan syarat fungsi invers dipenuhi. Amati Gambar 15.
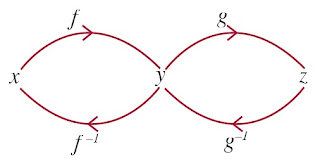 |
| Gambar 15. Fungsi komposisi dapat memiliki invers. |
Diketahui, fungsi f dan g keduanya bijektif. Fungsi f memetakan x ke y
dan fungsi g memetakan y ke z. Oleh karena f dan g bijektif maka balikan
fungsi f adalah f–1 dan balikan fungsi g adalah g–1 . Amati bahwa fungsi komposisi g ° f memetakan x ke z sehingga balikan g ° f, yaitu (g ° f)–1 memetakan z ke x. Dari Gambar 15. tampak bahwa f–1 memetakan z ke y dan f–1 memetakan y ke x. Dengan demikian, pemetaan komposisi f–1 ° g–1 memetakan z ke x. Jadi, invers fungsi komposisi (g ° f) adalah :
(g ° f)–1(x) = (f–1 ° g–1)(x)
Analog dengan cara tersebut, invers fungsi komposisi (f ° g) adalah :
(f ° g)–1(x) = (g–1 ° f–1)(x)
Contoh Soal 13 :
Diketahui f (x) = 3x2 – 6 dan g (x) = 3x – 19. Tentukan
a. (f ° g)–1 (x) b. (g ° f)–1 (x)
Pembahasan :
• f ° f–1 (x) = x
f (f–1 (x)) = x
3 (f–1 (x))2 – 6 = x
(f–1 (x))2 = 
f–1 (x) = 
• g ° g–1 (x) = x
g (g–1 (x)) = x
3 (g–1 (x)) – 19 = x
g–1 (x) = 
a. (f ° g)–1 (x) = g–1 ° f–1 (x) = g–1 (f–1 (x))
b. (g ° f)–1 (x) = f–1 (g–1(x)) = f–1 
Contoh Soal 14 :
Jika f (x) =  , g–1 (x) =
, g–1 (x) =  , dan h (x) = g {f (x)}, tentukan
, dan h (x) = g {f (x)}, tentukan
h–1 (x).
Pembahasan :
Pertama, hitung g(x) sebagai berikut.
g–1 (x) =  ↔ x g–1 (x) = 1 – x
↔ x g–1 (x) = 1 – x
↔ x g–1 (x) + x = 1
↔ x (g–1 (x) + 1) =1
↔ x = 
Jadi, g (x) = 
Kemudian, hitung h(x) sebagai berikut.
h (x) =g {f (x)}
↔ h (x) = 
↔ h (x) =
↔ h (x) =
Hitung h–1(x) sebagai berikut.
h (x) =  ↔ x h (x) = x – 1 ↔ x h (x) – x = – 1
↔ x h (x) = x – 1 ↔ x h (x) – x = – 1
↔ x (h (x) – 1) = – 1 ↔ x = 
Jadi, h–1 (x) = 
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/05/fungsi-komposisi-dan-fungsi-invers-aljabar-contoh-soal-sifat-pengertian-relasi-injektif-surjektif-pembahasan-penyelesaian-cara-menentukan-menghitung-matematika.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
No comments:
Post a Comment