Blognya anak tuban sejati: Pengertian Lengkap Gerak Rotasi beserta Contoh Soal

Pengertian Lengkap Gerak Rotasi beserta Contoh Soal

Dalam kehidupan sehari-hari, Anda banyak menjumpai contoh gerak rotasi. Bumi berotasi pada sumbunya untuk bergerak mengelilingi Matahari dalam orbit yang bentuknya elips. Demikian juga Bulan yang berotasi pada sumbunya untuk bergerak mengelilingi Bumi. Mobil yang bergerak mengelilingi suatu sudut juga bergerak dalam busur melingkar. Kajian tentang gerak melingkar telah Anda pelajari di artikel lainnya. Dalam subbab ini, akan dibahas gerak benda yang berotasi pada sumbunya yang ditinjau secara umum menggunakan fungsi turunan dan integral.

1. Posisi Sudut dan Perpindahan Sudut

Di Kelas X, Anda telah mempelajari bahwa posisi sudut suatu partikel yang bergerak melingkar dinyatakan sebagai θ dengan satuannya dalam radian atau derajat. Apabila partikel tersebut berpindah, perpindahannya disebut perpindahan sudut.

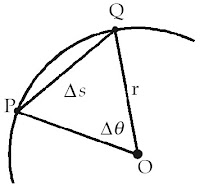Gambar 1. Sebuah partikel yang berpindah dari titk P ke titik Q dalam lintasan lingkaran.

Perhatikanlah Gambar 1. di atas. Gambar tersebut menunjukkan sebuah partikel yang bergerak dalam lintasan berbentuk lingkaran berjari-jari R. Partikel tersebut berpindah dari titik P ke titik Q dengan jarak perpindahan linear Δs = s_Q – s_P dan perpindahan sudut Δθ = θ_Q – θ_P. Oleh karena itu, dapat dinyatakan hubungan sebagai berikut.

Δθ = Δs / r (1-1)

dengan:

Δθ = perpindahan sudut (rad),

Δs = perpindahan linear (m), dan

r = jari-jari lingkaran (m).

2. Kecepatan Sudut

Berdasarkan definisi kecepatan, kecepatan sudut adalah perubahan posisi sudut partikel per satuan waktu. Kecepatan sudut juga terbagi atas dua, yaitu kecepatan sudut rata-rata dan kecepatan sudut sesaat. Analisa kedua jenis kecepatan tersebut ditinjau dari perhitungan integral dan turunan akan dibahas pada bagian berikut.

a. Kecepatan Sudut Rata-Rata

Perpindahan sudut yang dilakukan oleh partikel yang bergerak melingkar merupakan fungsi waktu. Dengan demikian, dapat dituliskan θ = θ (t). Perhatikanlah Gambar 2.

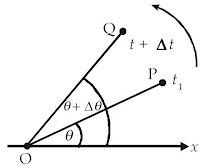Gambar 2. Perpindahan sudut sebesar Δθ selama selang waktu Δt

Posisi sudut benda di titik P pada saat t dinyatakan sebagai θ . Kemudian, partikel tersebut berpindah selama selang waktu Δt sejauh Δθ sehingga pada saat t + Δt, partikel berada di titik Q dengan posisi sudut θ + Δθ . Perpindahan sudut partikel tersebut adalah :

Δθ = (θ + Δθ) − θ

Dengan demikian, kecepatan sudut partikel dapat dituliskan sebagai berikut.

$\bar{\omega}=\frac{\left ( \theta -\Delta \theta \right )-\theta }{\left ( t-\Delta t \right )-t}=\frac{\Delta \theta }{\Delta t}$ (1-2)

Oleh karena θ bersatuan derajat, radian, atau putaran, ω pun dapat bersatuan derajat/sekon, radian/sekon, atau putaran per sekon.

Apabila perpindahan sudut partikel tersebut dibuat grafik hubungan antara posisi sudut (θ ) terhadap waktu (t), seperti Gambar 3.

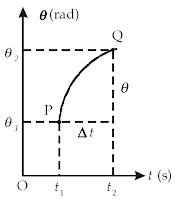Gambar 3. Perpindahan sudut sebesar Δθ selama selang waktu Δt pada partikel yang bergerak melingkar.

Anda dapat melihat bahwa kecepatan sudut rata-rata dinyatakan sebagai perubahan posisi selama selang waktu tertentu.

b. Kecepatan Sudut Sesaat

Perhatikanlah grafik posisi sudut terhadap waktu pada Gambar 4.

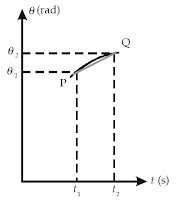Gambar 4. Grafik posisi sudut,θ , terhadap waktu, t, kecepatan sudut rata-rata, $\overline{\omega }=\frac{\Delta \theta }{\Delta t}$

Apabila selang waktu perpindahan partikel yang bergerak melingkar menuju nol, kemiringan garis yang menyatakan kecepatan sudut rata-rata partikel akan semakin curam. Dengan demikian, kecepatan sudut sesaat dapat didefinisikan sebagai.

$\omega =\lim_{\Delta t\rightarrow t}\bar{\omega }=\lim_{\Delta t\rightarrow t}\frac{\Delta \theta }{dt}$ (1-3)

atau :

$\omega =\frac{d\theta }{dt}$ (1-4)

dengan kalimat lain dapat dinyatkan bahwa ω merupakan turunan pertama dari fungsi posisi sudut terhadap waktu. Satuan kecepatan sudut sesaat dinyatakan dalam radian/sekon.

Contoh Soal 1 :

Posisi sudut suatu titik pada roda dinyatakan oleh θ = (3t² – 8t + 10) rad dengan t dalam sekon. Tentukanlah:

a. posisi sudut titik tersebut pada saat t = 2 sekon,

b. kecepatan sudut rata-rata selama 10 sekon pertama, dan

c. kecepatan sudut titik pada saat t = 10 sekon.

Kunci Jawaban :

Diketahui: θ = (3t² – 8t + 10) rad.

a. Posisi sudut titik pada saat t = 2 sekon adalah :

θ = 3t² – 8t + 10 = 3(2)² – 8(2) + 10 = 6 rad.

b. Tentukan lebih dahulu posisi sudut titik pada saat t = 0 dan t = 10 s.

t = 10 s → θ = 3(10)² – 8(10) + 10 = 230 rad

t = 0 → θ = 3(0)² – 8(0) + 10 = 10 rad

Δθ = 230 – 10 = 220 rad.

Untuk selang waktu Δt = 10 sekon, kecepatan sudut rata-rata adalah

$\omega =\frac{\Delta \theta }{\Delta t}=\frac{220}{10}=20\: rad/s$

c. Kecepatan sudut sesaat sebagai fungsi waktu ditentukan sebagai berikut.

$\omega =\frac{d\theta }{dt}=\frac{d}{dt}\left ( 3t^{2}-8t+10 \right )=6t-8$

Kecepatan sudut sesaat titik pada t = 10 s adalah ω = 6t – 8 = 6(10) – 8 = 52 m/s.

Catatan Fisika :

Fly Wheel

Flywheel atau roda gila adalah sebuah roda berdiameter besar yang biasanya digunakan pada mesin mobil untuk menstabilkan gerak mesin melalui gerak rotasi yang dilakukan oleh roda gila tesebut. [2]

Fly Wheel atau roda gila adalah sebuah roda berdiameter besar yang biasanya digunakan pada mesin mobil untuk menstabilkan gerak mesin melalui gerak rotasi yang dilakukan oleh roda gila tesebut.

3. Menentukan Posisi Sudut dari Fungsi Kecepatan Sudut

Fungsi posisi sudut dapat ditentukan dengan cara mengintegralkan persamaan sudut sebagai fungsi waktu. Cara ini sama dengan cara menentukan posisi suatu benda dari pengintegralan fungsi kecepatan benda yang telah dibahas pada subbab A. Dari Persamaan (1-4) Anda telah mengetahui bahwa :

$\omega \left ( t \right )=\frac{d\theta }{dt}\rightarrow d\theta =\omega \left ( t \right )dt$

Apabila persamaan tersebut diintegralkan, akan dapat dituliskan persamaan integral sebagai berikut :

persamaan integral fungsi kecepatan benda

(1-5)

dengan θ₀ = posisi sudut awal (rad atau derajat).

Perhatikanlah grafik pada Gambar 5. Oleh karena integral adalah penjumlahan yang kontinyu, nilai :

$\int_{0}^{t}\omega \left ( t \right )dt$

sama dengan luas daerah di bawah kurva grafik ω terhadap t.

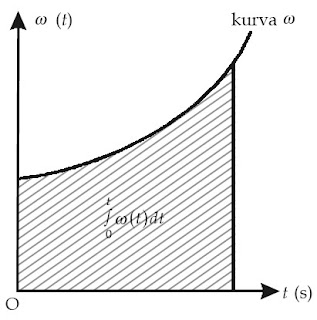Gambar 5. Posisi sudut partikel sama dengan daerah di bawah kurva.

4. Percepatan Sudut

Analogi dengan percepatan pada gerak linear, definisi percepatan sudut pada gerak melingkar adalah perubahan kecepatan sudut per satuan waktu. Pembahasan mengenai percepatan sudut juga terbagi atas dua, yaitu percepatan sudut rata-rata dan percepatan sudut sesaat.

a. Percepatan Sudut Rata-Rata

Kecepatan sudut pada saat t adalah sebesar ω dan pada saat t + Δt adalah sebesar ω + Δω. Percepatan sudut rata-rata partikel tersebut dapat dinyatakan sebagai :

$\alpha =\frac{\left ( \omega +\Delta \omega \right )-\omega }{\left ( t-\Delta t \right )-t}=\frac{d\omega }{dt}$ (1-6)

atau :

$\alpha =\frac{d\omega }{dt}$ (1-7)

dengan satuan percepatan sudut α adalah dalam rad/s².

b. Percepatan Sudut Sesaat

Percepatan sudut sesaat didefinisikan sebagai limit percepatan sudut rata-rata untuk selang waktu yang sangat kecil atau Δt menuju nol. Secara matematis, persamaannya dituliskan sebagai berikut.

Catatan Fisika :

Rotor Helikopter

Boeing CH-47 Chinook. [3]

Kecepatan sudut rotor helikopter (baling-baling yang terdapat di bagian ekor helikopter) dapat diubah dengan cara memberinya percepatan sudut melalui sebuah kontrol yang terdapat di cockpit.

Contoh Soal 2 :

Sebuah roda berotasi pada suatu poros tertentu. Titik partikel pada roda tersebut memenuhi persamaan kecepatan sudut ω = 2t² – 3t + 8, dengan ω dalam rad/s dan t dalam sekon. Tentukanlah:

a. percepatan sudut rata-rata partikel untuk selang waktu t = 2 sekon sampai t = 6 sekon,

b. percepatan sudut awal partikel, dan

c. percepatan sudut partikel pada saat t = 6 sekon.

Kunci Jawaban :

Diketahui: ω = 2t² – 3t + 8.

a. Persamaan umum kecepatan sudut adalah ω = 2t² – 3t + 8 sehingga

untuk t₂ = 6 sekon, ω₂ = 2(6)² – 3(6) + 8 = 62 rad/s, dan

untuk t₁ = 2 sekon, ω₁ = 2(2)² – 3(2) + 8 = –6 rad/s.

Percepatan sudut rata-ratanya, diperoleh :

$\bar{\alpha }=\frac{\Delta \omega }{\Delta t}=\frac{\omega _{2}-\omega _{1}}{t _{2}-t _{1}}=\frac{\left ( 62\: rad/s \right )-\left ( -6\: rad/s \right )}{\left ( 6s-2s \right )}$

b. Percepatan sudut sebagai fungsi waktu diperoleh dengan menerapkan persamaan berikut.

$\alpha =\frac{d\omega }{dt}=\frac{d}{dt}\left ( 2t^{2}-3t+8 \right )=4t-3$

Percepatan sudut awal partikel (pada t = 0) adalah α = –3 rad/s².

c Percepatan sudut partikel pada saat t = 6 sekon adalah α = 4(6) – 3 = 21 rad/s².

Catatan Fisika :

Roda Gerinda

Roda gerinda digunakan dalam industri untuk mengasah alat-alat berat.Roda gerinda ini mengandung material pengasah dan berotasi pada porosnya sehingga dapat mengasah permukaan alat-alat berat tersebut.

5. Menentukan Kecepatan Sudut dari Fungsi Percepatan Sudut

Berdasarkan Persamaan (1-7), Anda telah mengetahui bahwa percepatan sudut adalah turunan pertama dari fungsi kecepatan sudut. Oleh karena itu, apabila persamaan percepatan sudut sebagai fungsi waktu suatu partikel diintegralkan, akan diperoleh persamaan kecepatan sudutnya.

persamaan integral percepatan sudut sebagai fungsi waktu suatu partikel

(1-9)

dengan ω₀ = kecepatan sudut awal (rad/s)

Contoh Soal 3 :

Sebuah piringan hitam berputar dengan percepatan sudut α = (10 – 4t) rad/s² dengan t dalam sekon. Pada saat t = 0, sebuah titik berada pada sudut θ₀ = 0° dengan kecepatan sudut awal ω0 = 4 rad/s. Tentukan:

a. persamaan kecepatan sudut, dan

b. posisi sudut sebagai fungsi waktu.

Kunci Jawaban :

Diketahui: α = (10 – 4t) rad/s², θ 0 = 0°, dan ω 0 = 4 rad/s.

persamaan kecepatan sudut posisi sudut sebagai fungsi waktu

6. Gerak Melingkar Beraturan dan Gerak Melingkar Berubah Beraturan

Pada gerak melingkar beraturan, kecepatan sudut partikel tetap atau tidak bergantung pada waktu. Oleh karena itu, dari Persamaan (1-4) didapatkan persamaan gerak melingkar beraturan sebagai berikut.

$\omega =\frac{d\theta }{dt}\rightarrow d\theta =\omega dt$

Apabila setiap ruas diintegralkan, dapat dituliskan :

persamaan integral gerak melingkar beraturan

(1-10)

dengan θ₀ = posisi sudut saat t = 0 sekon (rad).

Pada gerak melingkar berubah beraturan, kecepatan sudut partikel berubah terhadap waktu (ω merupakan fungsi waktu) dan partikel bergerak melingkar dengan percepatan sudut, α , konstan. Oleh karena itu, dari Persamaan (1-7) didapatkan persamaan gerak melingkar berubah beraturan sebagai berikut.

$\alpha =\frac{d\theta }{dt}\rightarrow d\theta =\alpha dt$

Apabila ruas kanan dan ruas kiri persamaan diintegralkan, didapatkan :

persamaan integral gerak melingkar berubah beraturan

(1-11)

dengan 0 ω = kecepatan sudut awal (rad/s)

Apabila Persamaan (6-4) diintegralkan, akan diperoleh posisi sudut partikel sebagai berikut.

$\omega \left ( t \right ) =\frac{d\theta }{dt}\rightarrow d\theta =\omega \left ( t \right )dt$

Oleh karena (ωt) = ω₀ + αt maka pengintegralan persamaannya menjadi :

persamaan integral posisi sudut partikel

(1-12)

Jika θ₀ = 0, akan diperoleh persamaan :

$\theta =\omega _{0}\: t\: +\: \frac{1}{2}\: \alpha t$ (1-13)

Dari Persamaan (1–11) juga dapat diketahui bahwa :

$t=\frac{\left ( \omega _{t}-\omega _{0} \right )}{\alpha }$ (1-14)

Oleh karena itu jika Persamaan (1–14) disubstitusikan ke Persamaan (1–13) akan diperoleh :

$\theta =\omega _{0}\left ( \frac{\omega _{t}-\omega _{0}}{\alpha } \right )+\frac{1}{2}\alpha \left ( \frac{\omega _{t}-\omega _{0}}{\alpha } \right )^{2}$

ω_t² =ω₀² + 2αs (1-15)

Catatan Fisika :

1 putaran = 360° = 2π rad
1 rad = 180/π derajat = 57,3°
1 rpm = 1 rotasi per menit = 1 × (2π / 60 rad/s)

7. Analogi Gerak Translasi dan Gerak Rotasi

Gerak rotasi dan gerak translasi (persamaan gerak) memiliki banyak persamaan. Besaran gerak translasi memiliki hubungan dengan gerak rotasi. Hubungan tersebut menghasilkan bentuk rumus gerak rotasi yang bisa dianalogikan dengan gerak translasi, seperti terlihat pada Tabel 1. berikut.

Tabel 1. Tabel Analogi Gerak Translasi dan Gerak Rotasi

8. Percepatan Linear dan Percepatan Sudut

Perhatikan Gambar 6. berikut.

Gambar 6. Percepatan linear dan percepatan sudut.

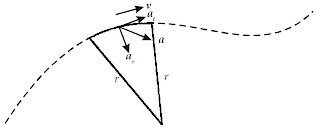
Titik P mengalami percepatan linear (a) yang terdiri atas percepatan tangensial (at) dan percepatan sentripetal (as), serta percepatan sudut (α ). Percepatan tangensial adalah komponen percepatan menurut arah garis singgung.

Percepatan sentripetal terjadi akibat perubahan arah vektor kecepatan dan arah percepatan sentripetal yang arahnya tegak lurus vektor kecepatan (menuju pusat lingkaran). Hubungan antara besaran-besaran tersebut adalah sebagai berikut.

(1-17)

Contoh Soal 4 :

Piringan hitam bergerak melingkar dengan kecepatan sudut 32 rad/s. Kemudian, kecepatannya berkurang menjadi 2 rad/s setelah 10 sekon.

a. Berapakah percepatan sudut meja jika dianggap konstan?

b. Jika radius meja putar adalah 10 cm, berapakah besar percepatan tangensial dan percepatan sentripetal sebuah titik di tepi piringan pada saat t = 10?

c. Berapakah percepatan totalnya?

Kunci Jawaban :

Diketahui: ω 0= 32 rad/s, ω t = 2 rad/s, r = 10 cm, dan t = 10 s.

a. Kecepatan sudut awal diperoleh dari persamaan ω = ω 0 + at.

2 rad/s = 32 rad/s + α (10 s) atau α = –3 rad/s²

Tanda negatif menunjukkan bahwa putaran piringan hitam diperlambat.

b. Percepatan tangensial at sebuah titik yang terletak pada jarak r = 10 cm dari pusat rotasi adalah :

at = α r =(-3 rad/s²)(10 cm) = –30 cm/s² (diperlambat)

Percepatan sentripetal dihitung sebagai berikut

as = ω 2 r = (2 rad/s)²(10 cm) = 40 cm/s²

c. Percepatan total benda adalah.

$a=\sqrt{a_{t}\, ^{2}+a_{s}\, ^{2}}=\sqrt{\left ( 2,42\: cm/s^{2} \right )^{2}+\left ( 168\: cm/s^{2} \right )^{2}}=50\: cm/s^{2}$
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/pengertian-gerak-rotasi-kinematika-dan-dinamika-momen-gaya-inersia-kesetimbangan-benda-tegar-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!

Blognya anak tuban sejati

Pages

Pengertian Lengkap Gerak Rotasi beserta Contoh Soal

1. Posisi Sudut dan Perpindahan Sudut

2. Kecepatan Sudut

3. Menentukan Posisi Sudut dari Fungsi Kecepatan Sudut

4. Percepatan Sudut

7. Analogi Gerak Translasi dan Gerak Rotasi

8. Percepatan Linear dan Percepatan Sudut

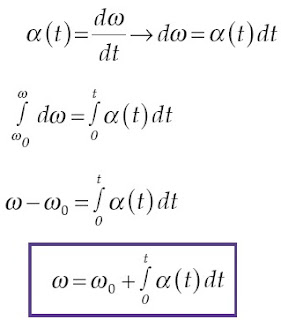
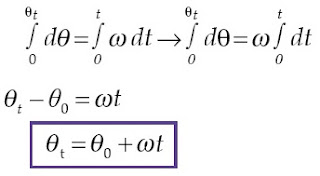
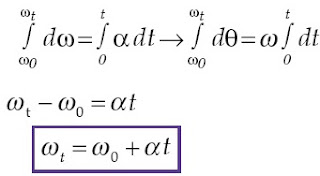
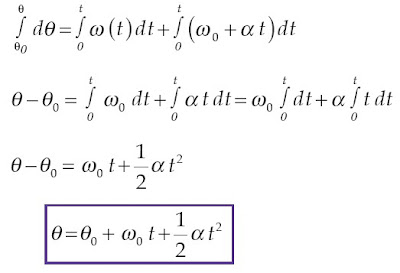
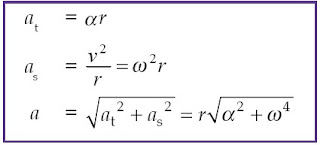
No comments:

Not Indonesian?

Search This Blog