Seseorang yang ingin menerbangkan
sebuah balon udara-panas akan memanaskan udara di dalam balon tersebut
agar balon dapat terbang ke angkasa. Pemanasan tersebut mengakibatkan
temperatur udara di dalam balon meningkat dan memaksa sebagian udara
keluar dari bagian bawah balon yang terbuka. Tahukah Anda mengapa balon
udara-panas tersebut hanya dapat terbang saat udara di dalamnya
dipanaskan? Penggunaan balon udara-panas merupakan salah satu contoh
aplikasi dari sifat gas saat energi kinetiknya meningkat dan kerapatan
rata-ratanya sama dengan udara di sekeliling balon sehingga balon dapat
melayang di langit. Apa sajakah sifat-sifat gas tersebut? Bagaimanakah
aplikasi sifat tersebut dalam teknologi? Anda dapat mengetahui jawaban
pertanyaan tersebut pada pembahasan Bab ini mengenai teori kinetik gas.

 (1–17)
(1–17)
 (1–18)
(1–18)



 (1–20)
(1–20)
 (1–21)
(1–21)

 (1–25)
(1–25)
 (1–26)
(1–26)

 (1–27)
(1–27)


a. Gas monoatomik
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/teori-kinetik-gas-persamaan-gas-ideal-prinsip-ekuipartisi-energi-hukum-gas-rumus-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
 |
| Gambar 1. Balon udara panas. [1] |
Pada bab ini, Anda akan diajak untuk dapat menerapkan konsep
termodinamika dalam mesin kalor dengan cara mendeskripsikan sifat-sifat
gas ideal monoatomik.
1. Gas Ideal
Anda tentu telah mengetahui bahwa setiap zat, baik itu zat padat, cair,
maupun gas, terdiri atas materi-materi penyusun yang disebut atom.
Sebagai partikel penyusun setiap jenis zat yang ada di Bumi dan di
seluruh alam semesta, atom-atom berukuran sangat kecil dan tidak dapat
dilihat, walaupun menggunakan alat yang paling canggih. Oleh karena itu,
gaya yang ditimbulkan oleh interaksi antar partikel dan energi setiap
partikel hanya dapat diamati sebagai sifat materi yang dibentuk oleh
sejumlah partikel tersebut secara keseluruhan. Analogi pernyataan ini
dijelaskan sebagai berikut. Misalkan, Anda memiliki sejumlah gas oksigen
yang berada di dalam tabung tertutup. Jika Anda ingin mengetahui
gaya-gaya yang bekerja pada setiap atom oksigen, Anda hanya dapat
mengamati perilaku seluruh gas oksigen yang ada di dalam tabung dan
menganggap bahwa hasil pengamatan Anda sebagai penjumlahan dari
gaya-gaya yang bekerja pada setiap atom gas oksigen.
Sifat mekanika gas yang tersusun atas sejumlah besar atom-atom atau
molekul-molekul penyusunnya dijelaskan dalam teori kinetik gas. Dalam
menjelaskan perilaku gas dalam keadaan tertentu, teori kinetik gas
menggunakan beberapa pendekatan dan asumsi mengenai sifat-sifat gas yang
disebut gas ideal.
Sifat-sifat gas ideal dinyatakan sebagai berikut.
- Jumlah partikel gas sangat banyak, tetapi tidak ada gaya tarik menarik (interaksi) antarpartikel.
- Setiap partikel gas selalu bergerak dengan arah sembarang atau acak.
- Ukuran partikel gas dapat diabaikan terhadap ukuran ruangan tempat gas berada.
- Setiap tumbukan yang terjadi antarpartikel gas dan antara partikel gas dan dinding bersifat lenting sempurna.
- Partikel gas terdistribusi merata di dalam ruangan.
- Berlaku Hukum Newton tentang gerak.
Pada kenyataannya, tidak ditemukan gas yang memenuhi kriteria gas ideal.
Akan tetapi, sifat itu dapat didekati oleh gas pada temperatur tinggi
dan tekanan rendah.
2. Hukum-Hukum tentang Gas
Teori kinetik gas membahas hubungan antara besaran-besaran yang
menentukan keadaan suatu gas. Jika gas yang diamati berada di dalam
ruangan tertutup, besaran-besaran yang menentukan keadaan gas tersebut
adalah volume (V), tekanan (p), dan suhu gas (T). Menurut proses atau
perlakuan yang diberikan pada gas, terdapat tiga jenis proses, yaitu
isotermal, isobarik, dan isokhorik. Pembahasan mengenai setiap proses
gas tersebut dapat Anda pelajari dalam uraian berikut.
a. Hukum Boyle
Perhatikanlah Gambar 1. berikut.
 |
| Gambar 1. (a) Gas di dalam tabung memiliki volume V1 dan tekanan P1. (b) Volume gas di dalam tabung diperbesar menjadi V2 sehingga tekanannya P2 menjadi lebih kecil. |
Suatu gas yang berada di dalam tabung dengan tutup yang dapat diturunkan
atau dinaikkan, sedang diukur tekanannya. Dari gambar tersebut dapat
Anda lihat bahwa saat tuas tutup tabung ditekan, volume gas akan
mengecil dan mengakibatkan tekanan gas yang terukur oleh alat pengukur
menjadi membesar. Hubungan antara tekanan (p) dan volume (V) suatu gas
yang berada di ruang tertutup ini diteliti oleh Robert Boyle.
Saat melakukan percobaan tentang hubungan antara tekanan dan volume gas
dalam suatu ruang tertutup, Robert Boyle menjaga agar tidak terjadi
perubahan temperatur pada gas (isotermal). Dari data hasil
pengamatannya, Boyle mendapatkan bahwa hasil kali antara tekanan (p) dan
volume (V) gas pada suhu tetap adalah konstan. Hasil pengamatan Boyle
tersebut kemudian dikenal sebagai Hukum Boyle yang secara matematis
dinyatakan dengan persamaan :
pV = konstan (1–1)
atau
p1V1
= p2V2 (1–2)
Dalam bentuk grafik, hubungan antara tekanan (p) dan volume (V) dapat dilihat pada Gambar 2.
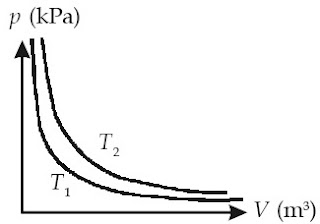 |
| Gambar 2. Grafik p-V suatu gas pada dua suhu yang berbeda, di mana T1>T2. |
b. Hukum Gay-Lussac
Gay-Lussac, seorang ilmuwan asal Prancis, meneliti hubungan antara
volume gas (V) dan temperatur (T) gas pada tekanan tetap (isobarik).
Perhatikanlah Gambar 3.
 |
| Gambar 3. Pada tekanan 1 atm, (a) gas bervolume 4 m3 memiliki temperatur 300 K, sedangkan (b) gas bervolume 3 m3 memiliki temperatur 225 K. |
Misalnya, Anda memasukkan gas ideal ke dalam tabung yang memiliki tutup
piston di atasnya. Pada keadaan awal, gas tersebut memiliki volume 4 m3 dan temperatur 300 K.
Jika kemudian pemanas gas tersebut dimatikan dan gas didinginkan hingga
mencapai temperatur 225 K, volume gas itu menurun hingga 3 m3.
Jika Anda membuat perbandingan antara volume terhadap suhu pada kedua
keadaan gas tersebut (V/T) , Anda akan mendapatkan suatu nilai konstan
(4/300 = 3/225 = 0,013).
Berdasarkan hasil penelitiannya mengenai hubungan antara volume dan
temperatur gas pada tekanan tetap, Gay-Lussac menyatakan Hukum
Gay-Lussac, yaitu hasil bagi antara volume (V) dengan temperatur (T) gas
pada tekanan tetap adalah konstan.
Persamaan matematisnya dituliskan sebagai berikut.
 |
| Gambar 4. Grafik hubungan V–T. |
V/T = Konstan (1–3)
atau
V1/T1 = V2/T2 (1–4)
Tokoh Fisika :
Robert Boyle ialah seorang ilmuwan Fisika berkebangsaan Inggris. Melalui
usaha dan kerja kerasnya, ia berhasil menemukan pompa vakum. Ia pun
menemukan Hukum Boyle berdasarkan penelitian yang dilakukan dengan
cermat dan teliti pada gas. Hukum Boyle banyak diterapkan dalam
teknologi dan telah memberikan banyak manfaat dalam kehidupan manusia.
Agar Anda dapat lebih memahami Hukum Boyle dan Hukum Gay- Lussac, lakukanlah kegiatan Percobaan Fisika Sederhana 1 :
Robert Boyle
(1627–1691)
 |
| Gambar 5. Robert Boyle. [2] |
Agar Anda dapat lebih memahami Hukum Boyle dan Hukum Gay- Lussac, lakukanlah kegiatan Percobaan Fisika Sederhana 1 :
Percobaan Fisika Sederhana 1
Membuktikan Hukum Boyle dan Hukum Gay-Lussac
Alat dan Bahan :
- Bola tembaga dengan katup dan alat pengukur tekanan
- Alat pengisap
- Pembakar bunsen
- Gelas kimia
- Penyangga kaki tiga
- Termometer
- Beban dan jangka sorong
- Klem dan statip
Prosedur :
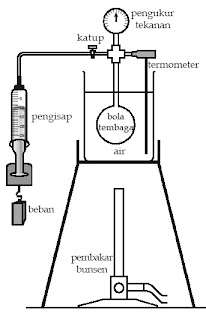
1. Susunlah alat-alat percobaan, seperti terlihat pada gambar.
2. Bukalah katup, kemudian tutuplah katup pada bola tembaga pada suhu
kamar. Catatlah nilai tekanan gas di dalam bola tembaga yang ditunjukkan
oleh alat pengukur tekanan. Catatlah kedua nilai besaran tersebut ke
dalam tabel berikut.
No
|
Suhu (°C)
|
Tekanan (mmHg)
|
3. Benamkan bola tembaga ke dalam air es. Pastikan jumlah es yang
terdapat di dalam gelas kimia cukup banyak sehingga dicapai suhu stabil
sistem antara 0 –10° C. Pastikan juga bahwa bola tembaga tidak menyentuh
dasar gelas kimia dan air es menutupi seluruh bola tembaga.
4. Masukkan termometer ke dalam gelas kimia (perhatikan agar termometer tidak menyentuh bola tembaga dan dasar gelas kimia).
5. Setelah temperatur stabil, catatlah nilai temperatur dan tekanan tersebut ke dalam tabel.
6. Nyalakanlah pembakar bunsen. Kemudian, catatlah nilai tekanan dan
temperatur untuk setiap kenaikan tekanan yang ditunjukkan oleh alat
pengukur tekanan.
7. Lakukanlah langkah ke-6 sampai air di dalam gelas kimia mendidih.
8. Bagaimanakah hubungan antara suhu dan tekanan yang Anda peroleh dari data pengamatan?
9. Sesuaikan hasil data pengamatan Anda dengan Hukum Gay-Lussac? Jika
tidak sesuai, dapatkah Anda menjelaskan bagian apa yang menyebabkan
timbulnya perbedaan tersebut? Diskusikanlah dengan teman-teman kelompok
dan guru Fisika Anda.
B. Percobaan Boyle
1. Dalam percobaan Boyle ini, digunakan pompa yang memiliki katup yang
dapat ditutup. Sejumlah gas yang telah ditentukan banyaknya,
terperangkap di dalam pompa. Temperatur gas selalu sama dengan
temperatur kamar, sedangkan tekanan gas diubah dengan cara
menggantungkan beban yang berbeda-beda pada silinder pompa.
2. Bukalah katup di ujung pompa, kemudian aturlah pompa agar menunjukkan volume udara sebesar 9 cm3. Tutuplah katup pompa. Catatlah tekanan dan volume gas pada tabel berikut.
Massa (kg)
|
Gaya (N)
|
Tekanan
(N/m2)
|
Volume (m3)
|
1/ Volume
(1/m3)
|
0
|
0
|
0
|
9 × 10–6
|
1,11 ×
105
|
0,2
|
||||
0,4
|
||||
...
|
Oleh karena tekanan gas yang diperhitungkan dalam percobaan ini adalah
tekanan netto gas, Anda dapat menganggap tekanan udara luar pada keadaan
awal gas adalah nol.
3. Tambahkan beban 200 g ke dalam pengisap. Bacalah volume gas dalam
pengisap. Catatlah massa dan volume tersebut ke dalam tabel di atas.
4. Lakukanlah langkah k-3 hingga massa beban mencapai 1,6 kg.
5. Hitunglah tekanan di dalam pengisap dengan cara membagi gaya yang diberikan pada pengisap dengan luas penampang pengisap.
6. Ukurlah diameter pengisap menggunakan jangka sorong, kemudian hitunglah luas penampang pengisap tersebut.
7. Bagaimanakah hubungan antara tekanan dan volume pada percobaan tersebut?
8. Sesuaikah hasil data pengamatan Anda dengan Hukum Boyle?
c. Hukum Charles
Seorang ilmuwan Perancis lainnya, Charles, menyatakan hubungan antara
tekanan (p) terhadap temperatur (T) suatu gas yang berada pada volume
tetap (isokhorik). Hasil penelitiannya kemudian dikenal sebagai Hukum
Charles yang menyatakan hasil bagi tekanan (p) dengan temperatur (T)
suatu gas pada volume tetap adalah konstan.
Persamaan matematis dari Hukum Charles dinyatakan dengan :
 |
| Gambar 6. Grafik p-T suatu gas pada volume yang berbeda. |
P/T = Konstan (1–5)
atau
p1/T1 = p2/T2 (–6)
Anda dapat melakukan kegiatan Percobaan Fisika Sederhana 2 berikut secara berkelompok untuk lebih memahami Hukum Charles.
Percobaan Fisika Sederhana 2
Memahami Hukum Charles
Alat dan Bahan :
- Termometer
- Air
- Gelas kimia
- Pemanas
- Manometer
- Batang pengaduk
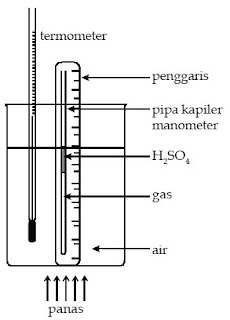
- Susunlah alat-alat dan bahan percobaan, seperti tampak pada gambar.
- Catatlah suhu awal dan perbedaan tinggi yang ditunjukkan manometer.
- Nyalakan pemanas, kemudian catatlah perbedaan tinggi raksa dalam kolom manometer setiap kenaikan suhu 5°C.
- Agar suhu air dalam gelas kimia merata, aduklah air tersebut dengan batang pengaduk.
- Diskusikan hubungan antara temperatur terhadap tekanan gas. Sesuaikah data hasil pengamatan Anda dengan Hukum Charles?
d. Persamaan Keadaan Gas Ideal
Pada proses isobarik, tekanan gas tetap, sedangkan volume dan temperatur
gas berubah. Demikian juga dalam proses isokhorik dan isotermal,
terdapat satu variabel atau besaran gas yang berada dalam keadaan tetap,
sedangkan kedua variabel gas lainnya berubah. Bagaimanakah jika ketiga
besaran yang menyatakan keadaan gas tersebut (tekanan, volume, dan suhu)
berubah?
Dari ketiga hubungan antara tekanan, volume, dan suhu gas yang
didapatkan dari Hukum Boyle dan Hukum Gay-Lussac dapat diturunkan suatu
persamaan yang disebut persamaan keadaan gas ideal. Secara matematis,
persamaan keadaan gas ideal dinyatakan dengan persamaan :
PV/T = Konstan (1–7)
atau
p1V1/T1 = p2V2/T2 (1–8)
Oleh karena setiap proses yang dilakukan pada gas berada dalam ruang
tertutup, jumlah molekul gas yang terdapat di dalam ruang tersebut dapat
ditentukan sebagai jumlah mol gas (n) yang jumlahnya selalu tetap. Anda
tentu sudah mengetahui bahwa mol adalah suatu besaran yang digunakan
untuk menyatakan massa suatu zat dalam gram yang besarnya sama dengan
jumlah molekul zat tersebut. Dengan demikian, persamaan keadaan gas
ideal dapat dituliskan menjadi :
pV/T = nR (1–9)
atau
pV = nRT (1–10)
dengan :
n = jumlah mol gas,
R = tetapan umum gas = 8,31 × 103 J/kmolK (SI) = 8,31 J/molK,
p = tekanan (N/m2),
V = volume (m3), dan
T = temperatur (K).
Dari definisi mol zat yang menyatakan bahwa :
jumlah mol = massa / massa relatif molekul
atau
n = m / Mr
Persamaan (1–10) dapat dituliskan menjadi :
pV = (m/Mr) RT (1–11)
Anda telah mempelajari bahwa massa jenis suatu zat adalah perbandingan
antara massa dengan volume zat tersebut. Oleh karena itu, dari Persamaan
(1–11) dapat diperoleh persamaan massa jenis gas :
ρ = m/V = p Mr/RT (1–12)
Menurut prinsip Avogadro, satu mol gas mengandung jumlah molekul gas
yang sama. Jumlah molekul gas ini dinyatakan dengan bilangan Avogadro
(NA) yang besarnya sama dengan 6,02 × 1023 molekul/mol. Dengan demikian, Persamaan (1–12) dapat dinyatakan menjadi :
pV = (N/NA) RT
atau
pV = N(R/NA) T (1–13)
dengan:
N = Banyak partikel gas, dan
NA = Bilangan avogadro = 6,02 × 1023 molekul/mol
Oleh karena nilai pada Persamaan (1–13) merupakan suatu nilai tetapan yang disebut konstanta Boltzmann, k, di mana k = 1,38 × 10-23 J/K maka persamaan keadaan gas ideal dapat juga dituliskan menjadi persamaan berikut.
pV = NkT (1–14)
Catatan Fisika :
Dalam keadaan standar (STP), yaitu tekanan p = 1 atm = 1 × 105 Pa, dan suhu gas t = 0° C atau T = 273 K, maka setiap n = 1 mol (gas apa saja) memiliki volume 22,4 liter.
Contoh Soal 1 :
Setetes raksa berbentuk bola memiliki jari-jari, r = 0,4 mm. Berapa
banyak atom raksa dalam tetesan tersebut jika diketahui Mr raksa = 202
kg/kmol dan massa jenis raksa ρ = 13.600 kg/m3?
Kunci Jawaban :
Diketahui: r = 0,4 mm, Mr = 202 kg/kmol, dan ρ = 13.600 kg/m3.
Massa raksa:
m = ρ V = ρ (4/3 π r3)
m = 13.600 kg/m3 × 4/3 x π × (0,4 × 10-3 m)3
m = 3,6 × 10–6 kg = 3,6 × 10-3 g
Jumlah mol raksa:
n = m / Mr = (3,6 x 10-3 / 202) mol = 1,78 × 10-5 mol.
Banyak atom raksa N = n NA = (1,78 × 10-5) (6,02 × 1023) = 1,07 × 1019 atom.
Contoh Soal 2 :
Sebuah silinder mengandung 20 liter gas pada tekanan 2,5 × 106 Pa. Keran
yang ada pada silinder dibuka sampai tekanannya turun menjadi 2,0 × 106
Pa, kemudian keran ditutup. Jika suhu dijaga tetap, berapakah volume
gas yang dibebaskan pada atmosfer bertekanan 1 × 105 Pa?
Kunci Jawaban :
Diketahui pada keadaan awal:
V1 = 20 L = 20 × 10–3 m3 dan p1 = 2,5 × 106 Pa
Keadaan akhir:
V2 = volume semestinya dan p2 = 2,0 ×
106 Pa.
Dengan menggunakan rumus p1V1
= p2V2 atau V2 = (p1/p2)
V1, maka :
V2 = (2,5 x 106
Pa / 2,0 x 106 Pa) x 20 L = 25 L pada tekanan p2
Gas yang keluar dari silinder
adalah 25 L – 20 L = 5 L pada tekanan p2. Oleh karena tekanan udara
luar 1 × 105 Pa, ΔV gas yang 5 L tersebut, di udara luar menjadi:
p2 ( ΔV) = P3V3
(2,0 × 106 Pa)(5 L) = (1
× 105 Pa)V3
V3 = 100 L.
Dengan demikian, volume gas yang dibebaskan adalah sebesar 100 L.
Seorang siswa ingin menerapkan hukum Boyle untuk menentukan tekanan
udara luar dengan menggunakan peralatan, seperti tampak pada gambar. Ia
mendapatkan bahwa ketika h = 50 mm, V = 18 cm3 dan ketika h = 150 mm, V = 16 cm3. Berapa mmHg tekanan udara luar di tempat siswa tersebut melakukan percobaan?
Kunci Jawaban :
Diketahui: h1 = 50 mm, V1 = 18 cm3,
h2 = 150 mm, dan V2 = 16 cm3.
Sesuai dengan sifat bejana
berhubungan, tekanan gas dalam V adalah:
• Keadaan 1: p1 = (p0
+ h1) mmHg = (p0 + 50) mmHg ...... (a)
• Keadaan 2: p2 = (p0
+ h2) mmHg = (p0 + 150) mmHg .... (b)
Menurut hukum Boyle: p2
V2 = p1 V1 atau p2 = (V1/V2)p1
= (18/16)p1 .... (c)
Substitusikan Persamaan (c) ke
Persamaan (b) sehingga diperoleh :
(18 cm3/16 cm3) p1
= p0 + 150 mm → p1 = (18 cm3/16 cm3) (p0
+ 150 mm)
Dengan memerhatikan Persamaan (a),
diperoleh:
(18 cm3/16 cm3) (p0
+ 150 mm) = (p0 + 50mm)
16 cm3( p0) +
16 cm3 (150 mm) = 18p0 + 18 cm3 (50 mm)
2 p0 = 16 cm3
(150 mm) – 18 cm3 (50 mm)
p0 = 750 mmHg
Tekanan udara luar adalah 750 mmHg atau 75 cmHg.
Contoh Soal 4 :
Menurut teori kinetik gas, tekanan gas dalam ruang tertutup:
1. Berbanding lurus dengan energi kinetik rata-rata partikel.
2. Berbanding terbalik dengan volume gas dalam ruang.
3. Berbanding lurus dengan jumlah partikel gas.
4. Berbanding terbalik dengan kuadrat kecepatan partikel gas.
Pernyataan-pernyataan yang benar adalah ....
a. 1 dan 2
b. 1 dan 3
c. 1, 2, dan 3
d. 2, 3, dan 4
e. 1, 3, dan 4
Kunci Jawaban :
Jawab: c
B. Prinsip Ekuipartisi Energi
Pada subbab A, Anda telah mempelajari hubungan antara variabel-variabel
yang menyatakan keadaan suatu gas dalam ruangan tertutup. Untuk
mengamati keadaan gas tersebut, dapat dilakukan dengan dua cara, yaitu
cara makroskopis dan mikroskopis. Jika Anda mengamati keadaan suatu gas
dalam ruang tertutup berdasarkan besaran-besaran yang dapat dilihat atau
diukur secara langsung, Anda dikatakan melakukan pengamatan secara
makroskopis. Namun, jika pengamatan yang Anda lakukan berdasarkan pada
variabel atau besaran yang tidak dapat dilihat atau diukur secara
langsung, Anda dikatakan melakukan pengamatan secara mikroskopis.
Pengamatan keadaan gas secara makroskopis telah Anda lakukan dan
pelajari pada subbab A. Pada subbab B ini, Anda akan mempelajari keadaan
gas yang diamati secara mikroskopis serta hubungan antara besaran
makroskopis dan besaran mikroskopis.
1. Tinjauan Tekanan Secara Mikroskopis
Berdasarkan sifat-sifat gas ideal, Anda telah mengetahui bahwa setiap
dinding ruang tempat gas berada, mendapat tekanan dari tumbukan
partikel-partikel gas yang tersebar merata di dalam ruang tersebut.
Cobalah Anda amati gerak satu partikel yang berada di dalam ruang
berbentuk kubus dengan panjang rusuk kubus L. Massa partikel tersebut
adalah m dan kecepatan partikel menurut arah sumbu-x dinyatakan sebagai vx (perhatikan Gambar 7).
 |
| Gambar 6. Sebuah partikel bergerak dengan kecepatan vx dalam ruang berbentuk kubus berusuk L. |
Jika partikel gas ideal tersebut menumbuk dinding ruang, tumbukan yang
terjadi adalah tumbukan lenting sempurna. Oleh karena itu, jika
kecepatan awal partikel saat menumbuk dinding A adalah +vx, kecepatan akhir partikel setelah terjadinya tumbukan dinyatakan sebagai - vx. Perubahan momentum (Dpx) yang dialami partikel adalah Dpx = pakhir – pawal
= -mvx - (mvx) = -2mvx.
Setelah menumbuk dinding A, partikel gas ideal tersebut menumbuk dinding
B. Demikian seterusnya, partikel gas tersebut akan bergerak bolak-balik
menumbuk dinding A dan dinding B. Dengan demikian, Anda dapat
menghitung selang waktu antara dua tumbukan yang terjadi pada dinding A
dengan persamaan :
Dt = 2L / vx (1–15)
Pada saat partikel gas tersebut menumbuk dinding, partikel memberikan gaya sebesar Fx pada
dinding. Pada pelajaran mengenai momentum, Anda telah mempelajari bahwa
besarnya gaya yang terjadi pada peristiwa tumbukan sama dengan laju
perubahan momentumnya (F = Dp / Dt). Dengan demikian, besar gaya Fx tersebut dapat diketahui sebagai berikut.
Fx = mvx2
/ L (1–16)
Jika di dalam ruang berbentuk kubus tersebut terdapat sejumlah N
partikel gas, yang kecepatan rata-rata seluruh molekul gas tersebut
dinyatakan dengan vx, gaya yang dialami dinding dinyatakan sebagai Ftotal. Dengan demikian, Persamaan (1–16) dapat dinyatakan menjadi :
Anda dapat mencari besarnya tekanan (p) yang dilakukan oleh gaya total (Ftotal) yang dihasilkan oleh N partikel gas ideal tersebut pada dinding A.
p = Ftotal
/ A
Oleh karena luas dinding adalah perkalian antara dua panjang rusuk dinding tersebtu (A = L2 maka persamaan tekanan pada dinding dapat ditulis dengan :
atau ;
pV = Nmvx2 (1–19)
dengan:
p = tekanan pada dinding, dan
V = volume ruang.
Dalam tinjauan tiga dimensi (tinjauan ruang), kecepatan rata-rata gerak
partikel merupakan resultan dari tiga komponen arah kecepatan menurut
sumbu-x ( ), sumbu-y (
), sumbu-y (  ), dan sumbu-z (
), dan sumbu-z (  ), yang besarnya sama. Oleh karena itu, dapat dituliskan
), yang besarnya sama. Oleh karena itu, dapat dituliskan  dengan
dengan  . Jika setiap komponen pada kedua ruas penamaan kecepatan tersebut dikuadratkan, dapat dituliskan :
. Jika setiap komponen pada kedua ruas penamaan kecepatan tersebut dikuadratkan, dapat dituliskan :
sehingga diperoleh,
Dengan demikian, Persamaan (1–19) dapat diubah menjadi :
atau
dengan:
N = banyaknya partikel gas,
m = massa 1 partikel gas,
v = kecepatan partikel gas, dan
V = volume gas.
Catatan Fisika :
Ukuran gelembung udara di dalam air berubah seiring dengan berubahnya
kedalam gelembung tersebut di dalam air. Jika seorang penyelam scuba
melepaskan gelembung udara di kedalaman air, tekanan air di kedalam
tersebut menentukan besarnya volume gelembung udara. Saat gelembung
udara tersebut naik ke permukaan, tekanan air menurun sehingga volume
gelembung udara pun membesar. (Sumber: Contemporary College Physics,
1993)
Gelembung Udara
 |
| Penyelam. [3] |
2. Hubungan Antara Tekanan Gas dan Energi Kinetik
Pada Persamaan (1–20), Anda telah menyatakan hubungan antara besaran
tekanan, volume, dan suhu (besaran makroskopis) suatu gas dengan besaran
mikroskopis (massa, jumlah, dan kecepatan) partikel gas tersebut.
Dari pelajaran sebelumnya, Anda juga telah mempelajari bahwa setiap
benda yang bergerak memiliki energi kinetik. Bagaimanakah hubungan
antara ketiga variabel makroskopis gas (tekanan, volume, dan suhu)
terhadap energi kinetiknya?
Perhatikanlah kembali Persamaan (1–18) dan Persamaan (1–21). Jika Persamaan (1–18) dituliskan menjadi:
p= NkT / V,
dan Persamaan (1–21) dituliskan sebagai
p = (1/3) (Nmv2 / V)
maka dapat diturunkan persamaan :
p= NKT / V = (1/3) (Nmv2 / V)
1/3 mv2 = kT (1–22)
Oleh karena EK = 1/2 mv2, maka Persamaan (1–22) dapat dituliskan menjadi :
2/3 (1/2 mv2) = kT
sehingga diperoleh,
2/3 EK = kT (1–23)
dan
EK = 2/3 kT (1–24)
Dari Persamaan (1–24) Anda dapat menyatakan bahwa energi kinetik gas
berbanding lurus dengan temperaturnya. Jadi, jika temperatur gas naik,
energi kinetiknya akan membesar. Demikian juga sebaliknya, jika suhu gas
turun, energi kinetiknya akan mengecil.
Jika energi kinetik Persamaan (1–24) dituliskan sebagai EK = 3
(1/2 kT), besaran 1/2 kT disebut juga sebagai derajat kebebasan gas.
Apakah derajat kebebasan gas itu? Derajat kebebasan berhubungan dengan
kebebasan partikel gas untuk bergerak di dalam ruang. Jadi, jika energi
kinetik suatu gas dinyatakan sebagai 3/2 kT, Anda dapat mengatakan bahwa
gas tersebut memiliki 3 derajat kebebasan menurut sumbu-x, sumbu-y, dan
sumbu-z. Derajat kebebasan ini berlaku untuk gas monoatomik, seperti
Helium (He), Argon (Ar), dan Neon (Ne). Semakin tinggi suhu suatu gas,
energi kinetiknya akan semakin besar. Secara fisis, meningkatnya energi
kinetik gas tersebut berhubungan dengan meningkatnya jumlah derajat
kebebasan yang dimilikinya. Pada gas-gas diatomik, seperti H2, N2,
dan O2, energi kinetiknya pada suhu rendah adalah 3/2 kT, pada suhu sedang 5/2 kT, dan suhu tinggi 7/2 kT.
Derajat kebebasan gas-gas diatomik pada suhu rendah diperoleh dari
kebebasan gerak partikel-partikelnya saat bertranslasi menurut sumbu-x,
sumbu-y, dan sumbu-z (v2 = vx2
+ vy2 + vz2 = 3vx2).
Pada suhu sedang, partikelpartikel gas diatomik tersebut dapat
bertranslasi dan berotasi. Namun, rotasi yang dialami partikel gas
menurut sumbu-x diabaikan karena nilainya sangat kecil. Dengan demikian,
energi kinetiknya, EK = 3/2 kT = 2 (1/2) kT = 5/2 kT. Jika temperatur
gas diatomik tersebut dinaikkan lagi hingga mencapai ±1.000 K, gerak
yang dilakukan oleh partikel-partikel gas adalah gerak translasi,
rotasi, dan vibrasi (bergetar pada sumbunya). Energi kinetik gas pada
suhu tinggi dinyatakan dengan :
EK = 3/2 kT + 2 (1/2) kT + 2 (1/2) kT + 7/2 kT
Anda telah mempelajari dari uraian di atas, bahwa jumlah derajat
kebebasan partikel gas menentukan energi yang dimiliki atau disimpan
oleh gas tersebut. Peninjauan energi partikel gas inilah yang dinamakan
Prinsip Ekuipartisi Energi oleh James Clerk Maxwell.
3. Energi Dalam Gas Ideal
Energi kinetik sejumlah partikel gas yang terdapat di dalam suatu ruang
tertutup disebut sebagai energi dalam gas (U). Jika di dalam ruangan
tersebut terdapat N partikel gas, energi dalam gas dituliskan dengan
persamaan :
U = NEK
Dengan demikian, energi dalam untuk gas monoatomik atau gas diatomik pada suhu rendah adalah :
U = NEK = 3/2 NkT
Adapun, energi dalam untuk gas-gas diatomik pada suhu sedang dinyatakan dengan :
U = 5/2 NkT
dan pada suhu tinggi, besar energi dalam gas adalah :
U = 7/2 NkT
4. Kecepatan Partikel Gas Ideal
Besaran lain yang dapat ditentukan melalui prinsip ekuipartisi energi
gas adalah akar dari rata-rata kuadrat kelajuan (vrms = root mean square
speed) gas, yang dirumuskan dengan :
Dari persamaan (1-24), Anda telah mengetahui bahwa EK = 3/2 kT. Dengan demikian dapat dirumuskan bahwa :
1/2 mv2 = 3/2 kT
v2 = 3kT / m
Berdasarkan persamaan gas ideal, Anda pun telah mengetahui bahwa pV =
NkT. Jika hanya terdapat satu mol gas, persamaan gas ideal tersebut
dapat dinyatakan pV = kT. Dengan demikian, Persamaan (1-25) dapat
dituliskan menjadi :
Anda tentu masih ingat bahwa massa jenis ( ρ ) adalah perbandingan
antara massa terhadap volume zat tersebut ( ρ = m / v) ). Oleh karena
itu, Persamaan (1–26) dapat dituliskan menjadi :
Berdasarkan Persamaan (1–27) tersebut, Anda dapat menyatakan bahwa massa
jenis gas berbanding terbalik dengan kelajuan partikelnya. Jadi, jika
massa jenis ( ρ ) gas di dalam ruangan tertutup besar, kelajuan partikel
gas tersebut akan semakin kecil.
Contoh Soal 5 :
Neon (Ne) adalah suatu gas monoatomik. Berapakah energi dalam 2 gram gas
neon pada suhu 50°C jika massa molekul relatifnya Mr = 10 g/mol?
Kunci Jawaban :
Diketahui: m = 2 gram, T = 50°C, dan Mr = 10 g/mol.
U = 3/2 nRT = (3/2) (m/Mr) (RT)
U = 3/2 x (2 g/10 g/mol) x 8,31 J/molK x (50 273) K = 805,24 J.
Contoh Soal 6 :
Sebuah tangki bervolume 2,4 m3 diisi dengan 2 kg gas. Tekanan dalam tangki 1,3 atm. Berapakah kecepatan efektif molekul-molekul gas ini?
Kunci Jawaban :
Diketahui: V = 2,4 m3, m = 2 kg, dan p = 1,3 atm.
v = 687,52 m/s.
Rangkuman :
1. Gas Ideal adalah gas yang memenuhi sifat-sifat berpartikel banyak,
antarpartikel tidak berinteraksi, arah gerak setiap partikel sembarang,
ukuran partikel terhadap ruang tempatnya dapat diabaikan, tumbukan
antarpartikel bersifat lenting sempurna, partikel gas terdistribusi
merata di seluruh ruang, dan berlaku Hukum Newton tentang gerak.
2. Hukum Boyle berlaku pada proses isotermal
pV = konstan
p1V1 = p2V2
3. Hukum Gay-Lussac berlaku pada proses isobarik
V/T = Konstan atau V1/T1 = V2/T2
4. Hukum Charles berlaku pada proses isokhorik
p/T = Konstan atau p1/T1 = p2/T2
5. Hukum Boyle-Gay Lussac merupakan penggabungan antara Hukum Boyle dan Hukum Gay- Lussac
pV/T = Konstan atau p1V1/T1 = p2V2/T2
6. Persamaan keadaan gas ideal
pV = nRT atau pT = NkT
7. Tekanan gas ideal
p = 1/3 (Nmv2/V)
8. Energi dalam gas ideal
a. Gas monoatomik
EK = 3/2 NkT = 3/2 nRT
b. Gas diatomik
1) Pada suhu rendah:
U = NEK = 3/2 NkT = 3/2 nRT
2) Pada suhu sedang:
U = NEK = 5/2 NkT = 5/2 nRT
3) Pada suhu tinggi:
U = NEK = 7/2 NkT = 7/2 nRT
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/teori-kinetik-gas-persamaan-gas-ideal-prinsip-ekuipartisi-energi-hukum-gas-rumus-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!


No comments:
Post a Comment