Menurut Hukum Kedua Newton, persamaan
gerak translasi benda diam bermassa m yang dikenai gaya F dan bergerak
dengan percepatan a adalah F = m x a. Demikian juga untuk benda dengan
momen inersia I yang bergerak rotasi dengan percepatan sudut α karena
adanya momen gaya τ, persamaannya adalah τ = I x α .
Hubungan antara momen gaya dan percepatan sudut pada gerak rotasi analog dengan Hukum Kedua Newton pada gerak translasi. Pada gerak rotasi, berlaku hubungan sebagai berikut.
τ= Iα (1–26)
dengan:
τ = momen gaya (Nm),
Kunci Jawaban :
Diketahui: ω 0 = 10 rad/s, ω = 70 rad/s, I = 4 kg m2, dan t = 3 s.

Kunci Jawaban :
Diketahui: d = 40 cm, ω = (5 + 20t) rad/s, m = 4 kg, dan I = 2/5 mR2.

Diketahui: R = 15 cm, massa katrol silinder M = 2 kg, dan massa ember m = 1 kg.
Σ F = ma
a. Berapakah percepatan yang dialami benda pejal tersebut?
Diketahui: Ibenda pejal = kMR2.
a. Menurut Hukum Kedua Newton pada gerak translasi, diperoleh hubungan :
Perhatikanlah roda delman, seperti terlihat pada Gambar 17.
Agar dapat berjalan, roda delman tersebut harus dapat menggelinding di
sepanjang jalan yang dilaluinya. Apakah gerak menggelinding itu? Gerak
menggelinding adalah perpaduan antara gerak rotasi dengan gerak
translasi. Perhatikanlah Gambar 18. Gerak translasi dicontohkan pada
Gambar 18a. Pada gambar tersebut, gaya F bekerja di pusat massa (PM)
roda sehingga roda berpindah atau bertranslasi.
Pada Gambar 18b, gaya F bekerja di jari-jari roda sehingga menyebabkan roda berotasi pada pusat massanya. Jika kedua jenis gerak yang dilakukan pada Gambar 18a dan 18b disatukan, roda akan menggelinding, seperti yang terlihat pada Gambar 18c.
Dalam kehidupan sehari hari, konsep menggelinding tanpa slip ini dapat Anda temukan pada desain ban kendaraan, misalnya mobil dan motor. Desain permukaan ban kendaraan dirancang sedemikian rupa agar gesekan yang ditimbulkan saat ban bersentuhan dengan jalan, dapat membuat roda menggelinding sempurna tanpa slip.
Pada Desain Ban Desain ban suatu kendaraan berbeda-beda, sesuai dengan kebutuhan kendaraan tersebut. Jika Anda perhatikan, ban yang digunakan oleh para pembalap Formula One memiliki permukaan yang lebih licin daripada ban mobil biasa, bahkan terkadang tidak bergerigi sama sekali. Menurut Anda, adakah gaya gesek yang ditimbulkan oleh ban mobil balap itu? Apabila dihubungkan dengan konsep menggelinding tanpa slip, apakah fungsi ban seperti yang digunakan oleh para pembalap tersebut? Untuk mendukung jawaban Anda, cobalah Anda cari informasi lebih lanjut mengenai kegunaan desain ban mobil balap dan perbandingannya dengan desain ban mobil biasa di perpustakaan, internet, dan sumber-sumber lainnya.
EK trans = ½ mv2
Sedangkan, pada benda yang berotasi murni, energi kinetiknya adalah energi kinetik rotasi, yaitu
EK rot = ½ Iω2 (1–27)
Pada benda yang menggelinding, gerak benda merupakan perpaduan
EK tot = EK trans + EK rot
a. Nyatakan kelajuan bola pada saat tiba di dasar bukit.
Kunci Jawaban :
Diketahui: m = M, r = R, dan I = kMR2.
Pada Bab 5, Anda telah mempelajari bahwa sebuah benda yang bergerak pada suatu garis lurus, memiliki momentum yang disebut momentum linear. Sekarang, bagaimana dengan benda yang berotasi? Pada benda yang melakukan gerak rotasi juga terdapat momentum yang disebut momentum sudut. Momentum sudut didefinisikan sebagai perkalian antara momen inersia dan kecepatan sudut. Secara matematis, ditulis sebagai berikut.
L = Iω (6–30)
dengan:
I = momen inersia (kgm2),
Momentum sudut merupakan besaran vektor karena memiliki besar dan arah. Arah momentum sudut dapat ditentukan dengan aturan tangan kanan, seperti yang ditunjukkan pada Gambar 20.
L = mvr (1–31)
Jika momen gaya luar sama dengan nol, berlaku Hukum Kekekalan Momentum Sudut, yaitu momentum sudut awal akan sama besar dengan momentum sudut akhir.
Secara matematis, pernyataan tersebut ditulis sebagai berikut.
I1ω1 + I2ω2
= I1ω1' + I2ω2 ' (1–32)
Dari Persamaan (1–32), dapat dilihat bahwa apabila I bertambah besar, ω akan semakin kecil. Sebaliknya, apabila ω semakin besar maka I akan mengecil. Prinsip ini diaplikasikan oleh pemain es skating dalam melakukan putaran (spinning). Saat akan memulai putaran badan, pemain es skating merentangkan lengannya (momen inersia pemain akan semakin besar karena jarak lengan dengan badan bertambah). Kemudian, ia merapatkan kedua lengannya ke arah badan agar momen inersianya mengecil sehingga putaran badannya akan semakin cepat (kecepatan sudutnya membesar).
Kunci Jawaban :
Diketahui: mmeja = M, rmeja = R, ωmeja = ω , mpiringan = m, dan rpiringan = R.
Mω = (M + m) ω '
 Kecepatan sudut akhir sistem adalah :
Kecepatan sudut akhir sistem adalah :

artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/pengertian-gerak-rotasi-kinematika-dan-dinamika-momen-gaya-inersia-kesetimbangan-benda-tegar-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
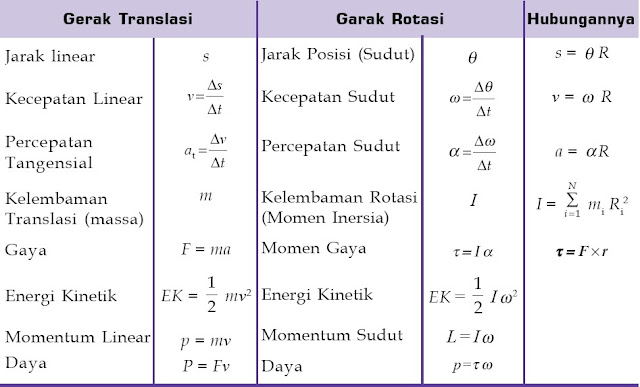
Analogi dan hubungan antara gerak translasi dan gerak rotasi dapat dilihat pada Tabel 3. berikut.
Tabel 3. Analogi Gerak Translasi dan Rotasi
1. Hubungan antara Momen Gaya dan Percepatan Sudut
Hubungan antara momen gaya dan percepatan sudut pada gerak rotasi analog dengan Hukum Kedua Newton pada gerak translasi. Pada gerak rotasi, berlaku hubungan sebagai berikut.
τ= Iα (1–26)
dengan:
τ = momen gaya (Nm),
I = momen inersia (kgm2), dan
α = percepatan sudut (rad/s2).
Catatan Fisika :
Obeng [11]
Mengendurkan atau mengencangkan sebuah sekrup memerlukan pemberian
percepatan sudut pada sekrup. Hal itu berarti memberikan torsi pada
sekrup. Pemberian torsi ini mudah dilakukan dengan menggunakan obeng
berjari-jari pegangan yang besar. Obeng ini akan menghasilkan lengan
pengungkit besar untuk gaya yang diberikan oleh tangan Anda. (Sumber:
Fisika Universitas, 2002)
Contoh Soal 11 :
Sebuah roda berputar dari kecepatan 10 rad/s menjadi 70 rad/s karena
mendapat momen gaya tetap dalam waktu 3 sekon. Jika momen kelembaman
roda 4 kg m2, tentukanlah besar momen gaya tersebut.
Kunci Jawaban :
Diketahui: ω 0 = 10 rad/s, ω = 70 rad/s, I = 4 kg m2, dan t = 3 s.
Contoh Soal 12 :
Sebuah bola pejal yang berdiameter 40 cm berotasi dengan poros yang
melalui pusat bola. Persamaan kecepatan sudut bola adalah (5 + 20t)
rad/s dengan t dalam sekon. Apabila massa bola 4 kg, tentukan momen gaya
yang bekerja pada bola.
Kunci Jawaban :
Diketahui: d = 40 cm, ω = (5 + 20t) rad/s, m = 4 kg, dan I = 2/5 mR2.
Catatan Fisika :
Torsi
Sejak dahulu, pengukuran massa benda dilakukan dengan cara
menyeimbangkan torsi antara dua lengan gaya suatu neraca yang dikenal
dengan nama neraca lengan. (Sumber: Conceptual physics, 1998)
Contoh Soal 13 :
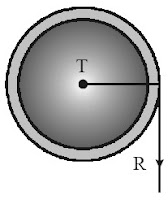
Sebuah silinder pejal berjari-jari 15 cm dan bermassa 2 kg dijadikan katrol untuk sebuah sumur, seperti tampak pada gambar. Batang yang dijadikan poros memiliki permukaan licin sempurna. Seutas tali yang massanya dapat diabaikan, digulung pada silinder. Kemudian, sebuah ember bermassa 1 kg diikatkan pada ujung tali. Tentukan percepatan ember saat jatuh ke dalam sumur.
Contoh Soal 13 :
Sebuah silinder pejal berjari-jari 15 cm dan bermassa 2 kg dijadikan katrol untuk sebuah sumur, seperti tampak pada gambar. Batang yang dijadikan poros memiliki permukaan licin sempurna. Seutas tali yang massanya dapat diabaikan, digulung pada silinder. Kemudian, sebuah ember bermassa 1 kg diikatkan pada ujung tali. Tentukan percepatan ember saat jatuh ke dalam sumur.
Kunci Jawaban :
Diketahui: R = 15 cm, massa katrol silinder M = 2 kg, dan massa ember m = 1 kg.
Berdasarkan persamaan momen gaya didapatkan :
τ= Iα
RT = I (a/R)
T = I a/R2 .... (a)
Berdasarkan Hukum Newton didapatkan :
Σ F = ma
mg – T = ma .... (b)
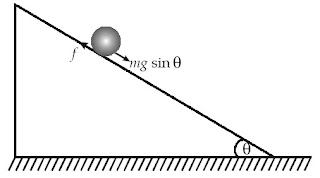
Sebuah benda pejal bermassa M dan berjari-jari R, memiliki momen inersia I = kMR2. Benda tersebut menggelinding pada suatu bidang miring dengan sudut kemiringan, seperti tampak pada gambar.
a. Berapakah percepatan yang dialami benda pejal tersebut?
b. Tentukanlah percepatan yang terjadi, jika benda itu berupa bola dengan momen inersia I =2/5 MR2, atau silinder dengan I =1/2 MR2.
Kunci Jawaban :
Diketahui: Ibenda pejal = kMR2.
a. Menurut Hukum Kedua Newton pada gerak translasi, diperoleh hubungan :
Mg sin θ – f = Ma atau Ma + f = Mg sin θ .... (a)
Berdasarkan prinsip rotasi terhadap pusat benda, berlaku hubungan :
τ=Iα → f R = kMR α→ f = kMa .... (b)
Substitusikan Persamaan (b) ke dalam Persamaan (a), diperoleh :
Ma + kMa = Mg sinθ → a = (gsinθ) / (k+1)
b. Untuk silinder dengan k = 1/2, diperoleh :

2. Energi dan Usaha dalam Gerak Rotasi
Perhatikanlah roda delman, seperti terlihat pada Gambar 17.
 |
| Gambar 17. Roda delman yang sedang berjalan merupakan salah satu contoh gerak menggelinding. [12] |
Pada Gambar 18b, gaya F bekerja di jari-jari roda sehingga menyebabkan roda berotasi pada pusat massanya. Jika kedua jenis gerak yang dilakukan pada Gambar 18a dan 18b disatukan, roda akan menggelinding, seperti yang terlihat pada Gambar 18c.
 |
| Gambar 18. (a) Roda bergerak translasi karena ditarik dengan gaya yang bekerja pada titik pusat massanya (PM). (b) Roda berotasi pada titik pusat massanya (PM). (c) Roda menggelinding. |
Dalam melakukan gerak menggelinding, dibutuhkan gaya gesek antara benda
dengan permukaan. Jika tidak ada gaya gesek maka benda tersebut akan
tergelincir atau slip (benda hanya melakukan gerak translasi).
Perhatikanlah Gambar 19.
Dari uraian gaya-gaya yang bekerja pada roda tersebut dapat Anda lihat
bahwa gaya normal N, gaya F, dan gaya berat ω bekerja pada titik pusat
massa roda. Gaya F menyebabkan benda bertranslasi. Gaya gesek f
menimbulkan momen gaya pada roda sebesar τ sehingga roda dapat berotasi
dan menggelinding tanpa slip. Dapat disimpulkan bahwa gaya gesek yang
bekerja pada benda, memegang peranan penting agar benda dapat
menggelinding sempurna tanpa slip.
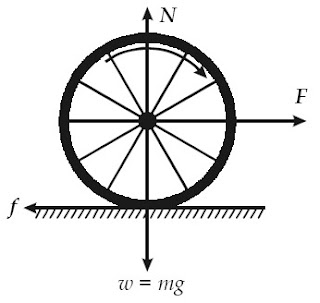 |
| Gambar 19. Sebuah bola pejal yang menggelinding tanpa slip pada suatu permukaan datar. |
Dalam kehidupan sehari hari, konsep menggelinding tanpa slip ini dapat Anda temukan pada desain ban kendaraan, misalnya mobil dan motor. Desain permukaan ban kendaraan dirancang sedemikian rupa agar gesekan yang ditimbulkan saat ban bersentuhan dengan jalan, dapat membuat roda menggelinding sempurna tanpa slip.
Percobaan Fisika Sederhana 2 :
Menganalisa Penerapan Konsep Menggelinding Pada Desain Ban Desain ban suatu kendaraan berbeda-beda, sesuai dengan kebutuhan kendaraan tersebut. Jika Anda perhatikan, ban yang digunakan oleh para pembalap Formula One memiliki permukaan yang lebih licin daripada ban mobil biasa, bahkan terkadang tidak bergerigi sama sekali. Menurut Anda, adakah gaya gesek yang ditimbulkan oleh ban mobil balap itu? Apabila dihubungkan dengan konsep menggelinding tanpa slip, apakah fungsi ban seperti yang digunakan oleh para pembalap tersebut? Untuk mendukung jawaban Anda, cobalah Anda cari informasi lebih lanjut mengenai kegunaan desain ban mobil balap dan perbandingannya dengan desain ban mobil biasa di perpustakaan, internet, dan sumber-sumber lainnya.
Diskusikan jawaban Anda tersebut bersama dengan teman-teman kelompok Anda serta guru Fisika Anda.
Ketika sedang menggelinding, benda memiliki energi kinetik yang terbagi
atas dua jenis, yaitu energi kinetik translasi dan energi kinetik
rotasi. Anda telah mengetahui pada benda yang bergerak translasi, energi
kinetiknya adalah energi kinetik translasi, yaitu
EK trans = ½ mv2
Sedangkan, pada benda yang berotasi murni, energi kinetiknya adalah energi kinetik rotasi, yaitu
EK rot = ½ Iω2 (1–27)
Pada benda yang menggelinding, gerak benda merupakan perpaduan
antara gerak translasi dan gerak rotasi. Oleh karena itu, energi kinetik yang
dimiliki benda adalah energi kinetik total, yaitu
EK tot = EK trans + EK rot
EK tot = ½ mv2
+ ½ Iω2 (1–28)
Jika resultan momen gaya luar yang bekerja pada benda sama dengan nol
(tidak ada momen gaya luar yang bekerja pada benda), pada gerak rotasi
tersebut berlaku Hukum Kekekalan Energi Mekanik, yang dituliskan sebagai
berikut.
ΔEP = ΔEK trans
+ ΔEK rot (1–29)
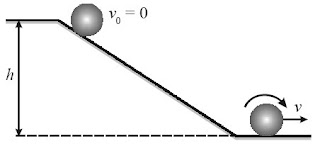
Sebuah benda pejal bermassa M, jari-jari R, dan momen inersia I = kMR2 (k adalah sebuah konstanta) menggelinding menuruni bidang miring, seperti tampak pada gambar.
a. Nyatakan kelajuan bola pada saat tiba di dasar bukit.
b. Jika benda pejal adalah bola (k = 2/5), berapakah kelajuan bola di dasar bukit?
c. Tentukan juga kelajuannya apabila benda tersebut adalah silinder (k = 1/2 ).
Kunci Jawaban :
Diketahui: m = M, r = R, dan I = kMR2.
Catatan Fisika :
Syarat agar suatu roda berjari-jari dan kelajuan sudut pusat massanya ω
dapat menggelinding tanpa slip adalah roda tersebut harus memiliki
kecepatan pusat massa vpm = ω.
3. Momentum Sudut dan Hukum Kekelan Momentum Sudut
Pada Bab 5, Anda telah mempelajari bahwa sebuah benda yang bergerak pada suatu garis lurus, memiliki momentum yang disebut momentum linear. Sekarang, bagaimana dengan benda yang berotasi? Pada benda yang melakukan gerak rotasi juga terdapat momentum yang disebut momentum sudut. Momentum sudut didefinisikan sebagai perkalian antara momen inersia dan kecepatan sudut. Secara matematis, ditulis sebagai berikut.
L = Iω (6–30)
dengan:
I = momen inersia (kgm2),
ω = kecepatan sudut (rad/s), dan
L = momentum sudut (kgm2/s).
Momentum sudut merupakan besaran vektor karena memiliki besar dan arah. Arah momentum sudut dapat ditentukan dengan aturan tangan kanan, seperti yang ditunjukkan pada Gambar 20.
 |
| Gambar 20. Arah putaran keempat jari menunjukkan arah rotasi, sedangkan ibu jari menunjukkan arah momentum sudut. |
Apabila jari-jari benda yang melakukan gerak rotasi jauh lebih kecil
dibandingkan dengan jarak benda itu terhadap sumbu rotasi r, momentum
sudut benda itu dinyatakan sebagai momentum sudut partikel yang secara
matematis dituliskan sebagai
L = mvr (1–31)
Jika momen gaya luar sama dengan nol, berlaku Hukum Kekekalan Momentum Sudut, yaitu momentum sudut awal akan sama besar dengan momentum sudut akhir.
 |
| Gambar 21. Benda pejal bermassa m yang bergerak dengan kecepatan v pada lingkaran berjari-jari r. Momentum sudutnya L = mvr. |
Lawal = Lakhir
Dari Persamaan (1–32), dapat dilihat bahwa apabila I bertambah besar, ω akan semakin kecil. Sebaliknya, apabila ω semakin besar maka I akan mengecil. Prinsip ini diaplikasikan oleh pemain es skating dalam melakukan putaran (spinning). Saat akan memulai putaran badan, pemain es skating merentangkan lengannya (momen inersia pemain akan semakin besar karena jarak lengan dengan badan bertambah). Kemudian, ia merapatkan kedua lengannya ke arah badan agar momen inersianya mengecil sehingga putaran badannya akan semakin cepat (kecepatan sudutnya membesar).
 |
| Gambar 22. Putaran badan (ω) dari pemain es skating ini bertambah cepat saat ia merapatkan kedua tangannya ke arah badan. [13] |
Contoh Soal 16 :
Diketahui sebuah piringan hitam bermassa m dan berjari-jari R. Piringan
hitam ini diletakkan di atas sebuah meja putar dengan jari-jari R dan
massa M yang sedang berputar dengan kecepatan sudut ω . Meja putar ini
dapat berputar dengan bebas tanpa ada momen gaya luar yang bekerja
padanya. Jika piringan hitam dan meja putar dapat dianggap sebagai
silinder homogen, berapakah kecepatan sudut akhir sistem?
Kunci Jawaban :
Diketahui: mmeja = M, rmeja = R, ωmeja = ω , mpiringan = m, dan rpiringan = R.
Gunakan Hukum Kekekalan Momentum Sudut, yaitu :
(momentum sudut awal = momentum sudut akhir)
Lmeja = Lmeja
+ Lpiringan → Imω = Imω2 + Ipω2
(1/2 MR2)ω=(1/2
MR2+1/2 mR2)
Mω = (M + m) ω '
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/pengertian-gerak-rotasi-kinematika-dan-dinamika-momen-gaya-inersia-kesetimbangan-benda-tegar-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!






No comments:
Post a Comment