Program Linear dan Sistem Pertidaksamaan Linear Dua Variabel

Para pedagang atau pengusaha tentu ingin memperoleh keuntungan maksimum. Sebelum melakukan transaksi ataupun pengambilan keputusan dalam usahanya, mereka pasti membuat perhitungan yang matang tentang langkah apa yang harus dilakukan. Oleh karena itu, diperlukan metode yang tepat dalam pengambilan keputusan pedagang atau pengusaha tersebut untuk memperoleh keuntungan maksimum dan meminimumkan kerugian yang mungkin terjadi.

Tujuan Pembelajaran :

1. Setelah mempelajari bab ini, diharapkan kalian dapat
2. menjelaskan sistem pertidaksamaan linear dua variabel dan penyelesaiannya;
3. menentukan fungsi tujuan (fungsi objektif) beserta kendala yang harus dipenuhi dalam masalah program linear;
4. menggambarkan kendala sebagai daerah pada bidang yang memenuhi sistem pertidaksamaan linear;
5. menentukan nilai optimum dari fungsi tujuan sebagai penyelesaian dari program linear;
6. menafsirkan nilai optimum yang diperoleh sebagai penyelesaian masalah program linear.

Pada pokok bahasan kali ini, kita akan membahas suatu metode untuk mengoptimalkan (memaksimumkan/meminimumkan) keuntungan atau biaya, yaitu program linear. Program linear banyak digunakan dalam kehidupan sehari-hari, misalnya dalam bidang ekonomi, perdagangan, dan pertanian.

Untuk mempelajari program linear, mari kita ingat kembali tentang cara menentukan himpunan penyelesaian pertidaksamaan linear dua variabel.

A. Sistem Pertidaksamaan Linear

1. Menyelesaikan Sistem Pertidaksamaan Linear Dua Variabel

Pada pembahasan kali ini, kita akan menentukan penyelesaian sistem pertidaksamaan linear dengan dua variabel menggunakan metode grafik. Metode grafik dimaksudkan untuk melihat secara visual gambaran tentang daerah penyelesaian dari pertidaksamaan linear yang berbentuk aljabar. Karena secara umum grafik pertidaksamaan linear seperti ax + by ≥ c, ax + by > c, ax + by < c, dan ax + by ≤ c berupa daerah yang dibatasi oleh garis ax + by = c maka langkah-langkah dalam mengambar grafik pertidaksamaan linear adalah:

a. menggambar grafik garis ax + by = c sebagai batas daerahnya;

b. menyelidiki daerah penyelesaian yang dimaksud apakah berada di sebelah kiri, sebelah kanan, di atas, atau di bawah garis batas yang telah dilukis.

Suatu hal yang harus diingat dalam menggambar grafik sebuah garis adalah menentukan dua titik sembarang pada garis itu kemudian menghubungkannya dengan sebuah garis lurus, sedangkan dua titik sembarang yang mudah perhitungannya adalah titik potong garis ax + by = c dengan sumbu X dan titik potong garis dengan sumbu Y. Titik potong dengan sumbu X mempunyai bentuk (..., 0), yakni dicapai saat nilai y = 0, dan titik potong dengan sumbu Y mempunyai bentuk (0, ...), yakni dicapai saat nilai x = 0.

Dari alasan-alasan di atas maka untuk menggambar daerah penyelesaian pertidaksamaan linear adalah sebagai berikut.

a. Gambar grafik garis lurus pembatasnya dengan mengisi format :

x	0	...
y	...	0
(x, y)	(0, ...)	(..., 0)

b. Menyelidiki daerah yang merupakan penyelesaian dengan mengambil salah satu titik yang mudah, yaitu (0, 0). Perhatikan contoh-contoh berikut.

Contoh Soal 1 :

Gambarlah daerah himpunan penyelesaian linear berikut pada bidang Cartesius.

a. 3x + 2y ≥ 6, dengan x, y ϵ R

b. 2x + y > – 4, dengan x, y ϵ R

Penyelesaian :

a. 3x + 2y ≥ 6, dengan x, y ϵ R

Untuk menentukan daerah penyelesaian pertidaksamaan linear di atas, langkah-langkah pengerjaannya adalah sebagai berikut.

1) Menggambar grafik garis lurus pembatasnya

a) Titik potong dengan sumbu X, berarti y = 0. Kita ubah pertidaksamaan menjadi persamaan 3x + 2y = 6 sehingga 3x + 2(0) = 6 ↔ 3x = 6 ↔ x = 2. Jadi, titik potong grafik dengan sumbu X adalah (2, 0).

b) Titik potong dengan sumbu Y, berarti x = 0. Kita ubah persamaan menjadi 3x + 2y = 6 ↔ 3(0) + 2y = 6 ↔ 2y = 6 ↔ y = 3. Jadi, koordinat titik potong grafik dengan sumbu Y adalah (0, 3).

Hal tersebut dapat disajikan dengan tabel berikut. 

x	0	2
y	3	0
(x, y)	(0, 3)	(2, 0)

Grafik 3x + 2y = 6 dapat diperoleh dengan membuat garis yang menghubungkan koordinat (0, 3) dan (2, 0) seperti pada Gambar 1 (a).

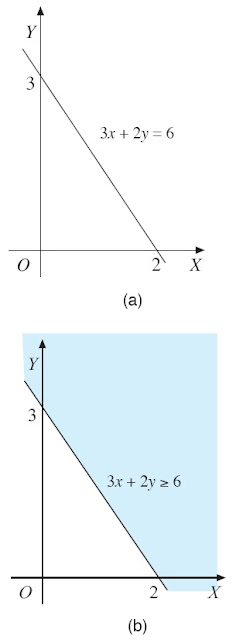Gambar 1. Garis yang menghubungkan koordinat pada grafik.

2) Menyelidiki daerah penyelesaian

Gambar 1 (a) merupakan grafik himpunan penyelesaian untuk persamaan 3x + 2y = 6. Tampak bahwa garis 3x + 2y = 6 membagi bidang Cartesius menjadi dua daerah, yaitu atas (kanan) garis dan bawah (kiri) garis. Untuk menentukan daerah himpunan penyelesaian 3x + 2y ≥ 6, ambil sembarang titik, misalnya (0, 0) dan substitusikan ke dalam pertidaksamaan linear 3x + 2y ≥ 6 sehingga diperoleh 3(0) + 2(0) ≥ 6 ↔ 0 ≥ 6 (pernyataan salah)

Karena titik (0, 0) terletak di bawah (kiri) garis dan setelah kita substitusikan ke pertidaksamaan itu, diperoleh pernyataan yang salah maka titik (0, 0) tidak berada pada daerah penyelesaian. Jadi, daerah penyelesaiannya adalah daerah yang diberi arsiran, seperti pada Gambar 1 (b).

b. 2x + y > – 4, x, y ϵ R

Langkah-langkah untuk menentukan daerah penyelesaian adalah sebagai berikut.

1) Menggambar grafik garis lurus pembatasnya

Dengan cara seperti di atas, diperoleh sebagai berikut.

Untuk x = 0 maka 2(0) + y = –4 ↔ y = –4.

Untuk y = 0 maka 2x + 0 = –4 ↔ x = –2

x	0	–2
y	–4	0
(x, y)	(0, –4)	(–2, 0)

Jadi, titik potong dengan sumbu koordinat adalah (0, –4) dan (–2, 0). Gambarnya terlihat pada Gambar 2. (a).

2) Menyelidiki daerah penyelesaian

Untuk menentukan daerah himpunan penyelesaian pertidaksamaan, kita ambil titik (0, 0). Dengan menyubstitusikan titik (0, 0) pada pertidaksamaan maka diperoleh 2(0) + 0 > –4 ↔ 0 > –4.

Terlihat bahwa pernyataan 0 > – 4 benar. Berarti, titik (0, 0) berada pada daerah penyelesaian, sedangkan garis 2x + y = –4 tidak memenuhi pertidaksamaan sehingga digambar putus-putus. Oleh karena titik (0, 0) berada di atas garis 2x + y = –4 maka daerah di atas garis diberi arsiran. Jadi, daerah penyelesaiannya adalah daerah yang diarsir, seperti pada Gambar 2. (b). Grafiknya dapat ditampilkan sebagai berikut.

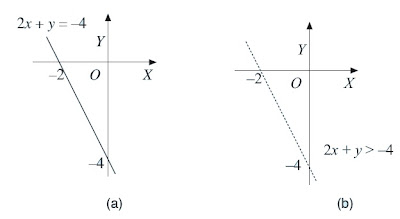Gambar 2. Grafik daerah himpunan penyelesaian pertidaksamaan.

Contoh Soal 2 :

Tentukan daerah himpunan penyelesaian yang memenuhi sistem pertidaksamaan berikut.

a. x ≥ 0; y ≥ 0; 2x + y ≤ 4; x, y ϵ R

b. x ≥ 0; y ≥ 0; x ≤ 3; x + y ≤ 5; x, y ϵ R

Pembahasan :

a. x ≥ 0; y ≥ 0; 2x + y ≤ 4

1) Kita cari titik potong 2x + y = 4 dengan sumbu koordinat Cartesius.

x	0	2
y	4	0
(x, y)	(0, 4)	(2, 0)

Untuk x = 0 → 2(0) + y = 4 ↔ y = 4.

Untuk y = 0 → 2x + 0 = 4 ↔ 2x = 4 ↔ x = 2.

Jadi, diperoleh titik potong (0, 4) dan (2, 0).

2) Grafik sistem pertidaksamaan linear tersebut tampak pada gambar di samping.

Pada grafik di samping,

a) penyelesaian x ≥ 0 tersebut berada di sebelah kanan sumbu Y maka yang kita arsir adalah daerah tersebut;

b) penyelesaian y ≥ 0 terletak di sebelah atas sumbu X maka kita arsir daerah tersebut;

c) untuk menyelidiki daerah himpunan penyelesaian dari pertidaksamaan 2x + y ≤ 4 maka ambil titik (0, 0), kemudian substitusikan ke 2x + y ≤ 4 sehingga diperoleh 2(0) + 0 ≤ 4 ↔ 0 ≤ 4.

Terlihat pernyataan di atas benar. Jadi, titik (0, 0) berada di dalam daerah penyelesaian sehingga daerah di mana titik (0, 0) berada, yaitu di bawah garis 2x + y = 4 kita arsir.

Dari ketiga himpunan penyelesaian yang diperoleh, dapat disimpulkan bahwa daerah penyelesaian dari sistem pertidaksamaan linear itu adalah irisan atau interseksi dari ketiga himpunan penyelesaian pertidaksamaan tersebut. Jadi, daerah yang diarsir adalah daerah penyelesaian dari sistem pertidaksamaan linear, seperti terlihat pada Gambar 3.

Gambar 3. Daerah yang diarsir adalah daerah penyelesaian dari sistem pertidaksamaan linear.

b. x ≥ 0; y ≥ 0; x ≤ 3; x + y ≤ 5; x, y ϵ R

1) Kita cari titik potong x + y = 5 dengan sumbu koordinat Cartesius.

Untuk x = 0 → 0 + y = 5 ↔ y = 5

Untuk y = 0 → x + 0 = 5 ↔ x = 5

Jadi, diperoleh titik potong (0, 5) dan (5, 0)

2) Grafik sistem pertidaksamaan linear tersebut adalah sebagai berikut.

Gambar 4. Grafik sistem pertidaksamaan linear.

Dari Gambar 4, tampak :

a) penyelesaian x ≥ 0 adalah daerah di sebelah kanan sumbu Y (daerah arsiran);

b) penyelesaian y ≥ 0 terletak di sebelah atas sumbu X (daerah arsiran);

c) penyelesaian x ≤ 3 adalah daerah di sebelah kiri garis x = 3;

d) penyelesaian pertidaksamaan x + y ≤ 5 adalah daerah di sebelah kiri (bawah garis x + y = 5);

e) titik potong garis x = 3 dan x + y = 5 dengan menyubstitusikan x = 3 ke persamaan x + y = 5 sehingga diperoleh y = 2. Jadi, titik potongnya adalah (3, 2).

Dengan demikian, himpunan penyelesaian dari sistem pertidaksamaan x ≥ 0, y ≥ 0, x ≤ 3, dan x + y ≤ 5 dengan x, y ϵ R adalah daerah segi empat OABC yang diarsir, seperti terlihat pada Gambar 4.

2. Model Matematika

Program linear adalah salah satu bagian dari matematika terapan yang berisikan pembuatan program untuk memecahkan berbagai persoalan sehari-hari. Persoalan-persoalan itu mengandung kendala atau batasan yang dapat diterjemahkan ke dalam model matematika. Model matematika adalah suatu hasil penerjemahan dari bahasa sehari-hari menjadi bentuk matematika berupa persamaan, pertidaksamaan, atau fungsi.

Jadi, program linear tersusun atas sistem pertidaksamaan linear. Penyelesaian dari pertidaksamaan linear berupa daerah himpunan penyelesaian. Di antara penyelesaian tersebut, terdapat penyelesaian terbaik yang disebut penyelesaian optimum. Penyelesaian optimum dapat berupa nilai maksimum atau nilai minimum dari suatu fungsi yang dinamakan fungsi objektif, fungsi sasaran atau fungsi tujuan. Untuk memahami lebih lanjut tentang program linear dan model matematika, perhatikan Aktivitas berikut.

Aktivitas :

Tujuan : Menentukan model matematika dari peristiwa kehidupan sehari-hari serta menyelesaikannya.

Permasalahan : Bagaimana cara merumuskan dalam bahasa matematika dan menyelesaikannya jika permasalahan disajikan dalam bentuk peristiwa sehari-hari?

Kegiatan : Simaklah persoalan berikut. Suatu perusahaan produsen mebel memproduksi dua jenis produk, yaitu meja makan dan lemari. Meja makan dijual dengan harga Rp650.000,00 dan lemari dijual dengan harga Rp1.100.000,00. Perusahaan itu memiliki target sebanyak 500 unit mebel produknya harus terjual dalam periode itu. Untuk memproduksi satu unit meja makan, diperlukan waktu 2 hari, sedangkan untuk memproduksi satu unit lemari, diperlukan waktu 5 hari. Waktu yang disediakan 150 hari. Berapa banyak meja makan dan lemari yang harus diproduksi oleh perusahaan itu agar pendapatannya maksimum?

1. Misalkan banyak meja makan dan lemari yang diproduksi dalam suatu variabel. Misalnya, banyak meja makan = x dan banyak lemari = y.

2. Susunlah pertidaksamaan-pertidaksamaan yang sesuai dengan kasus di atas.

a. Susun pertidaksamaan yang memuat banyak unit mebel yang diproduksi perusahaan itu.

b. Susun pertidaksamaan yang memuat waktu dalam proses produksinya.

c. Susun syarat bahwa banyak unit adalah bilangan cacah.

3. Susunlah suatu fungsi yang akan dimaksimumkan nilainya.

4. Dari pertidaksamaan-pertidaksamaan yang kalian peroleh, membentuk sistem pertidaksamaan. Gambarkan dalam bentuk grafik. Arsirlah daerah yang memenuhi sistem pertidaksamaan.

5. Bentuk apakah daerah himpunan penyelesaiannya (dalam grafik)?

6. Selidiki titik-titik sudutnya, dengan cara menyubstitusikan titik-titik itu ke dalam fungsi yang akan dimaksimumkan.

7. Dari langkah 6, berapakah jawaban dari permasalahan ini?

Kesimpulan : Apa yang dapat kalian simpulkan?

Setelah melakukan Aktivitas di atas, tentu kalian dapat membayangkan permasalahan sehari-hari ke dalam bahasa matematika. Agar kalian lebih jelas, pelajari contoh-contoh berikut.

Contoh Soal 3 :

Linda membeli 3 kue A dan 2 kue B di supermarket. Oleh karena itu, Linda harus membayar Rp3.400,00, sedangkan Wati membeli 2 kue A dan 3 kue B sehingga ia harus membayar Rp3.100,00. Jika harga sebuah kue A dan sebuah kue B masing-masing x rupiah dan y rupiah, buatlah model matematika dari masalah tersebut.

Jawaban :

Misalkan harga sebuah kue A adalah x dan harga sebuah kue B adalah y.

Untuk memudahkan pembuatan model matematika, kita buat tabel seperti tabel berikut.

Nama	Kue A	Kue B	Harga
Linda	3	2	3.400
Wati	2	3	3.100

Berdasarkan jumlah uang yang dibayarkan Linda maka diperoleh 3x + 2y = 3.400, sedangkan berdasarkan jumlah uang yang dibayarkan Wati, diperoleh 2x + 3y = 3.100. Karena x dan y menunjukkan harga barang maka nilai x dan y harus berupa bilangan real non-negatif sehingga x ≥ 0, y ≥ 0; x, y ϵ R.

Jadi, model matematika dari masalah di atas adalah :

3x + 2y = 3.400

2x + 3y = 3.100

x ≥ 0, y ≥ 0

x, y ϵ R

Contoh Soal 4 :

Luas lahan parkir 360 m². Luas rata-rata untuk sebuah mobil 6 m² dan untuk sebuah bus 24 m². Lahan parkir itu tidak dapat memuat lebih dari 25 kendaraan. Buatlah model matematika dari masalah tersebut.

Penyelesaian :

Misalkan banyak mobil adalah x dan banyak bus adalah y.

Masalah tersebut dapat disajikan dalam tabel berikut.

Dari tabel tersebut, diperoleh hubungan sebagai berikut.

6x + 24y ≤ 360

x + y ≤ 25

Karena x dan y menunjukkan banyaknya mobil dan bus maka x dan y harus berupa bilangan cacah.

Jadi, model matematika dari masalah tersebut adalah :

artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/05/program-linear-sistem-pertidaksamaan-linear-dua-variabel-contoh-soal-rumus-cara-menyelesaikan-model-matematika-pembahasan-praktikum.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!