1. Momen Gaya
Momen gaya (torsi) adalah sebuah besaran yang menyatakan besarnya gaya
yang bekerja pada sebuah benda sehingga mengakibatkan benda tersebut
berotasi. Anda telah mengetahui bahwa gaya akan menyebabkan terjadinya
perubahan gerak benda secara linear. Apabila Anda ingin membuat sebuah
benda berotasi, Anda harus memberikan momen gaya pada benda tersebut.
Apakah momen gaya itu? Agar Anda dapat memahami konsep momen gaya,
lakukanlah kegiatan Kerjakanlah Percobaan 1. berikut.
Percobaan Fisika Sederhana 1 :
Memahami Prinsip Momen Gaya
Ambillah satu penggaris. Kemudian, tumpukan salah satu ujungnya pada tepi meja. Doronglah penggaris tersebut ke arah atas atau bawah meja. Bagaimanakah gerak penggaris? Selanjutnya, tariklah penggaris tersebut sejajar dengan arah panjang penggaris. Apakah yang terjadi? Bandingkan kedua kejadian tersebut. Kesimpulan apakah yang Anda dapatkan? Diskusikanlah dengan teman Anda.
Saat Anda memberikan gaya F yang arahnya tegak lurus terhadap penggaris,
penggaris itu cenderung untuk bergerak memutar. Namun, saat Anda
memberikan gaya F yang arahnya sejajar dengan panjang penggaris,
penggaris tidak bergerak. Hal yang sama berlaku saat Anda membuka pintu.
Gaya yang Anda berikan pada pegangan pintu, tegak lurus terhadap daun
pintu sehingga pintu dapat bergerak membuka dengan cara berputar pada
engselnya. Gaya yang menyebabkan benda dapat berputar menurut sumbu
putarnya inilah yang dinamakan momen gaya. Definisi momen gaya secara
matematis dituliskan sebagai berikut.
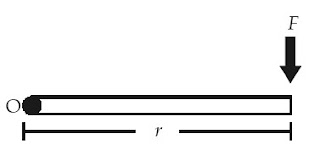 |
| Gambar 7. Sebuah batang dikenai gaya sebesar F yang tegak lurus terhadap batang dan berjarak sejauh r terhadap titik tumpu O. Batang tersebut memiliki momen gaya τ =r×F |
τ = r × F (1–18)
dengan:
r = lengan gaya = jarak sumbu rotasi ke titik tangkap gaya (m),
F = gaya yang bekerja pada benda (N), dan
τ = momen gaya (Nm).
Perhatikan Gambar 8.
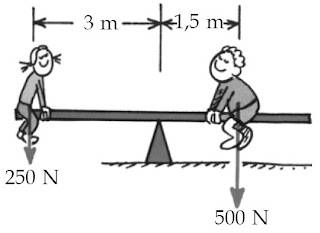 |
| Gambar 8. Jungkat-jungkit setimbang karena momen gaya pada kedua lengannya sama besar. [4] |
τ1 = r1 × F1
τ1 = (3 m)(250 N)
τ1 = 750 Nm
τ2 = (1,5 m)(500 N)
τ2 = 750 Nm
Dapat disimpulkan bahwa kedudukan setimbang kedua anak adalah akibat momen gaya pada kedua lengan sama besar.
Perhatikan Gambar 9.
 |
| Gambar 9. Momen gaya yang ditimbulkan oleh gaya yang membentuk sudut θ terhadap benda (lengan gaya = r). |
τ = rF sinθ (1-19)
Dari Persamaan (1–19) tersebut, Anda dapat menyimpulkan bahwa gaya yang
menyebabkan timbulnya momen gaya pada benda harus membentuk sudut θ
terhadap lengan gayanya. Momen gaya terbesar diperoleh saat θ = 90°
(sinθ = 1), yaitu saat gaya dan lengan gaya saling tegak lurus. Anda
juga dapat menyatakan bahwa jika gaya searah dengan arah lengan gaya,
tidak ada momen gaya yang ditimbulkan (benda tidak akan berotasi).
Perhatikanlah Gambar 10a dan 10b.
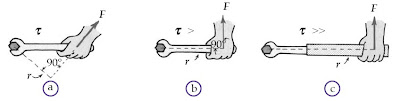 |
| Gambar 10. Semakin panjang lengan gaya, momen gaya yang dihasilkan oleh gaya akan semakin besar. [4] |
Arah gaya terhadap lengan gaya menentukan besarnya momen gaya yang
ditimbulkan. Momen gaya yang dihasilkan oleh gaya sebesar F pada Gambar
10b lebih besar daripada momen gaya yang dihasilkan oleh besar gaya F
yang sama pada Gambar 10a. Hal tersebut disebabkan sudut antara arah
gaya terhadap lengan gayanya. Momen gaya yang dihasilkan juga akan
semakin besar jika lengan gaya semakin panjang, seperti terlihat pada
Gambar 10c. Dengan demikian, dapat disimpulkan bahwa besar gaya F yang
sama akan menghasilkan momen gaya yang lebih besar jika lengan gaya
semakin besar. Prinsip ini dimanfaatkan oleh tukang pipa untuk membuka
sambungan antarpipa.
Sebagai besaran vektor, momen gaya τ memiliki besar dan arah. Perjanjian tanda untuk arah momen gaya adalah sebagai berikut.
a. Momen gaya, τ, diberi tanda positif jika cenderung memutar benda searah putaran jarum jam, atau arahnya mendekati pembaca.
b. Momen gaya, τ, diberi tanda negatif jika cenderung memutar benda
berlawanan arah putaran jarum jam, atau arahnya menjauhi pembaca.
Perjanjian tanda untuk arah momen gaya ini dapat dijelaskan dengan aturan tangan kanan, seperti yang ditunjukkan pada Gambar 11.
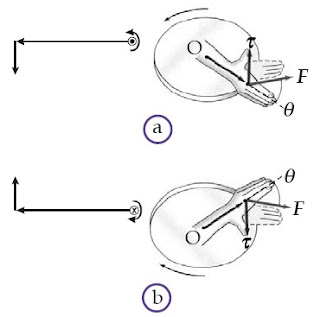 |
| Gambar 11. (a) Gaya yang menghasilkan momen gaya positif (mendekati pembaca) ditandai dengan titik. (b) Gaya yang menghasilkan momen gaya negatif (menjauhi pembaca) ditandai dengan tanda silang. [5] |
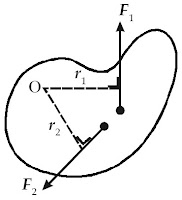 |
| Gambar 12. Pada benda bekerja dua gaya, yaitu F1 dan F2 yang menghasilkan momen gaya –τ1 dan +τ 2 . |
Perhatikan Gambar 12. Jika pada benda bekerja beberapa gaya, momen gaya
total benda tersebut adalah sebagai berikut. Besar τ yang ditimbulkan
oleh F1 dan F2 terhadap titik O adalah τ1 dan τ2. τ1 bernilai negatif karena arah rotasi yang ditimbulkannya berlawanan arah putaran jarum jam. Sedangkan, τ2 bernilai
positif karena arah rotasi yang ditimbulkannya searah putaran jarum
jam. Resultan momen gaya benda itu terhadap titik O dinyatakan sebagai
jumlah vektor dari setiap momen gaya. Secara matematis dituliskan :
τ total = Σ (r × F)
atau :
τtotal = τ1 + τ2
Contoh Soal 5 :
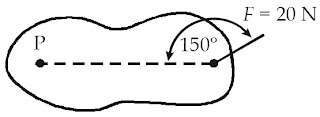
Pada sebuah benda bekerja gaya 20 N seperti pada gambar. Jika titik
tangkap gaya berjarak 25 cm dari titik P, berapakah besar momen gaya
terhadap titik P?
Diketahui: F = 20 N, r = 25 cm, dan θ = 150°.
τ = r F sinθ
τ = (0,25 cm)(20 N)(sin 150°)
τ = (0,25 cm)(20 N)(1/2)
τ = 2,5 Nm.
Contoh Soal 6 :
Sebuah gaya F = (3i + 5j) N memiliki lengan gaya r = (4i + 2j) m
terhadap suatu titik poros. Vektor i dan j berturut-turut adalah vektor
satuan yang searah dengan sumbu-x dan sumbu-y pada koordinat Kartesian.
Berapakah besar momen gaya yang dilakukan gaya F terhadap titik poros?
Kunci Jawaban :
Diketahui: F = (3i + 5j)N dan r = (4i + 2j)m.
τ = r × F = (4i + 2j)m × (3i + 5j)N = (4)(5) (k) Nm + (2)(3) (–k) Nm = 14 k
Jadi, besarnya momen gaya 14 Nm yang searah sumbu z.
Contoh Soal 7 :
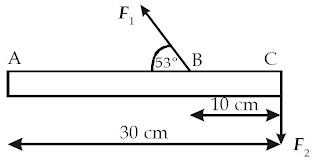
Batang AC yang panjangnya 30 cm diberi gaya seperti terlihat pada gambar. Jika BC = 10 cm dan F1 = F2 = 20 N, berapakah momen gaya total terhadap titik A?
Diketahui: r1 = 20 cm, F1 = F2 = 20 N, r2 = 30 cm, θ 1 =53°, dan θ 2 = 90°.
τ = –r1 F1 sinθ 1 + r2 F2 sinθ 2
τ = –(0,2 m)(20 N)(sin 53°) + (0,3 m)(20 N)(sin 90°)
τ = –3,2 Nm + 6 Nm = –2,8 Nm.
2. Momen Kopel
Kopel adalah pasangan dua buah gaya yang sejajar, sama besar, dan berlawanan arah. Kopel yang bekerja pada suatu benda akan mengakibatkan benda tersebut berotasi.
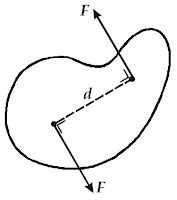 |
| Gambar 13. Kopel dari dua gaya yang sama besar dan berlawanan arah. |
M = F × d (1–21)
Perjanjian tandanya, yaitu jika kopel menyebabkan perputaran benda
searah putaran jarum jam, momen kopel (M) bernilai positif (mendekati
pembaca, ʘ).
Sebaliknya, apabila kopel menyebabkan perputaran benda berlawanan arah
dengan putaran jarum jam, momen kopel bernilai negatif (menjauhi pembaca
⊗).
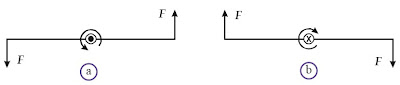 |
| Gambar 14. (a) Momen kopel positif mendekati pembaca diberi tanda ʘ. (b) Momen kopel negatif menjauhi pembaca diberi tanda ⊗. |
Contoh aplikasi momen kopel dalam keseharian terdapat pada pedal sepeda.
Kedua kaki akan memberikan gaya F yang sama pada pedal sepeda (panjang
pedal sama) dengan arah keduanya saling berlawanan.
 |
| Gambar 15. Kopel digunakan dalam mengayuh sepeda. [6] |
3. Momen Inersia
Sebuah benda yang berotasi pada sumbunya, cenderung untuk terus berotasi pada sumbu tersebut selama tidak ada gaya luar (momen gaya) yang bekerja padanya. Ukuran yang menentukan kelembaman benda terhadap gerak rotasi dinamakan momen inersia (I).
Momen inersia suatu bergantung pada massa benda dan jarak massa benda tersebut terhadap sumbu rotasi. Jika benda berupa partikel atau titik bermassa m berotasi mengelilingi sumbu putar yang berjarak r, momen inersia partikel itu dinyatakan dengan persamaan
I = mr2 (1–22)
Dari Persamaan (1–22) itu, Anda dapat menyimpulkan bahwa momen inersia suatu partikel berbanding lurus dengan massa partikel dan kuadrat jarak partikel tersebut terhadap sumbu rotasinya.
Dengan demikian, semakin jauh jarak poros benda (sumbu rotasinya), besar momen inersia benda tersebut akan semakin besar. Prinsip ini banyak digunakan dalam atraksi sirkus, misalnya atraksi berjalan pada seutas tali. Dalam atraksi tersebut, pemain akrobat membawa sepotong kayu panjang yang akan memperbesar momen inersianya sehingga ia dapat menyeimbangkan badannya saat berjalan pada tali tersebut.
 |
| Gambar 16. Kayu panjang yang dibawa pemain akrobat memperbesar momen inersianya sehingga ia dapat menyeimbangkan tubuhnya saat berjalan menyusuri tali. [7] |
Apabila terdapat banyak partikel dengan massanya masing-masing m1, m2,
dan m3, serta memiliki jarak masing-masing r1, r2,
dan r3 terhadap poros (sumbu rotasi), momen inersia
total partikel tersebut adalah penjumlahan momen inersia setiap
partikelnya. Secara matematis, dituliskan sebagai berikut.
Contoh Soal 8 :
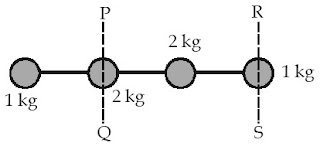
Empat partikel dihubungkan dengan batang kayu yang ringan dan massanya diabaikan seperti pada gambar berikut.
Jika jarak antarpartikel sama, yaitu 20 cm, berapakah momen inersia sistem partikel tersebut terhadap
a. poros PQ;
b. poros RS.
Kunci Jawaban :
Diketahui: m1 = 1 kg, m2 = 2 kg, m3 = 2 kg, m4 = 1 kg, dan r = 20 cm.
a. Momen inersia sistem terhadap poros PQ, berarti PQ sebagai sumbu rotasi
I = m1r12 + m2r22
+ m3r32 + m4r42
I = (1 kg)(0,2 m)2 + (2 kg)(0 m)2
+ (2 kg)(0,2 m)2 + (1 kg)(0,4 m)2 = 0,28 kgm2b. Momen inersia sistem terhadap poros RS, berarti RS sebagai sumbu rotasi
I = m1r12 + m2r22
+ m3r32 + m4r42
I = (1 kg)(0,6 m)2 + (2 kg)(0,4 m)2
+ (2 kg)(0,2 m)2 + (1 kg)(0 m)2 = 0,76 kgm2
Catatan Fisika :
Momen Inersia
Dengan mengukur perubahan yang kecil pada orbit satelit-satelit, ahli
geofisika dapat mengukur momen inersia Bumi. Hal ini menginformasikan
pada kita bagaimana massa planet-planet terdistribusi di bagian
dalamnya. Teknik yang sama juga telah digunakan di pesawat ruang angkasa
antarplanet untuk menyelidiki struktur dalam dari dunia-dunia lain.
(Sumber: Fisika Universitas, 2002)
Benda tegar adalah suatu benda yang memiliki satu kesatuan massa yang kontinu (tidak terpisahkan antara satu sama lain) dan bentuknya teratur. Pada benda tegar, massa benda terkonsentrasi pada pusat massanya dan tersebar pada jarak yang sama dari titik pusat massa benda. Oleh karena itu, momen inersia benda tegar dapat dihitung menggunakan teknik integral dengan persamaan
Benda tegar adalah suatu benda yang memiliki satu kesatuan massa yang kontinu (tidak terpisahkan antara satu sama lain) dan bentuknya teratur. Pada benda tegar, massa benda terkonsentrasi pada pusat massanya dan tersebar pada jarak yang sama dari titik pusat massa benda. Oleh karena itu, momen inersia benda tegar dapat dihitung menggunakan teknik integral dengan persamaan
I = ∫ r2dm (1–24)
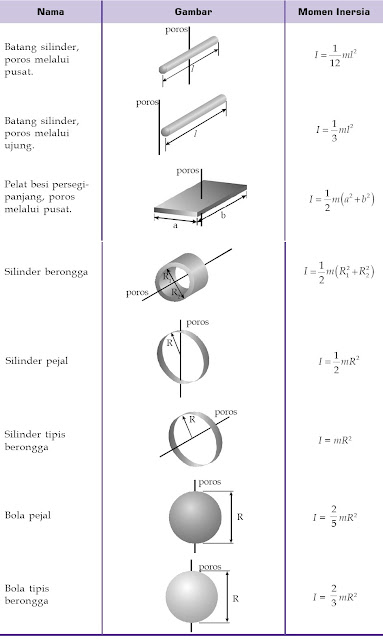
Momen inersia berbagai bentuk benda tegar berdasarkan sumbu rotasinya dituliskan pada tabel berikut.
Dalam kasus benda tegar, apabila momen inersia benda terhadap pusat massa Ipm diketahui,
momen inersia benda terhadap sumbu lain yang paralel dengan sumbu pusat
massa dapat dihitung menggunakan teori sumbu paralel, yaitu
I = Ipm + md2 (1–25)
dengan:
d = jarak dari sumbu pusat massa ke sumbu paralel (m), dan
m = massa benda (kg).
Contoh Soal 9 :.
Sebatang kayu silinder panjangnya 100 cm dan bermassa 800 g. Tentukan
momen inersia batang kayu itu, jika batang kayu tersebut berputar dengan
sumbu putarnya:
a. di tengah-tengah,
b. di ujung.
Kunci Jawaban :
Diketahui: l = 100 cm dan m = 800 g = 0,8 kg.
a. Momen inersia batang kayu dengan sumbu putarnya di tengah:
I = 1/12 ml2 = 1/12 (0,8 kg)(1 m)2 = 0,067 kgm2.
b. Momen inersia batang kayu dengan sumbu putarnya di ujung:
I = 1/3 ml2 = 1/3 (0,8 kg)(1 m)2 = 0,067 kgm2.
I = 1/3 ml2 = 1/3 (0,8 kg)(1 m)2 = 0,067 kgm2.
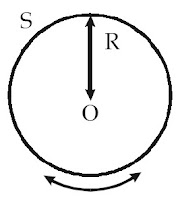
Contoh Soal 10 :
Sebuah piringan yang bermassa M dirotasikan dengan poros melalui pusat
massa O dan tegak lurus pada piringan. Momen inersia pusat massa
piringan tersebut adalah Ipm = 1/2 mR2 dengan
R adalah jari-jari piringan. Tentukanlah momen inersia piringan
tersebut jika poros digeser ke sisi piringan, yaitu di titik S yang
sejajar dengan poros semula.
Kunci Jawaban :
Diketahui: Ipm = 1/2 mR2 dan d = R.
Karena sumbu putar digeser sejauh d = R dari pusat massa, menurut teorema sumbu sejajar, momen inersia piringan adalah
Is = Ipm + md2 = 1/2 mR2 + mR2 = 3/2 mR2.
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/pengertian-gerak-rotasi-kinematika-dan-dinamika-momen-gaya-inersia-kesetimbangan-benda-tegar-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!

No comments:
Post a Comment