A. Kecepatan Linear dan Kecepatan Anguler
Sebuah benda dikatakan bergerak melingkar jika lintasan yang dilaluinya
berbentuk lingkaran. Pada pelajaran sebelumnya, Anda telah belajar
mengenai gerak lurus. Setiap benda yang bergerak selalu memiliki
kecepatan, walaupun kecepatan yang dimiliki setiap benda berbeda-beda.
Begitu pula dengan gerak melingkar, setiap benda yang bergerak melingkar
memiliki dua kecepatan, yakni kecepatan linear dan kecepatan anguler.
Kedua kecepatan ini tidaklah sama, akan tetapi penting dalam proses
gerak melingkar.
1. Kecepatan Linear
Coba Anda perhatikan benda-benda yang bergerak melingkar. Apa yang
menyebabkan benda tersebut berputar? Kecepatan apa saja yang dimiliki
benda tersebut ketika berputar? Kecepatan yang dimiliki benda ketika
bergerak melingkar dengan arah menyinggung lintasan putarannya disebut
kecepatan linear. Kecepatan linear akan selalu menyinggung lintasan
lingkaran yang memiliki panjang lintasan yang sama dengan keliling
lingkaran.
Δs = keliling lingkaran
Δs = 2πr (1-1)
dengan Δs adalah panjang lintasan yang ditempuh dan r adalah jari-jari lintasan yang berbentuk lingkaran.
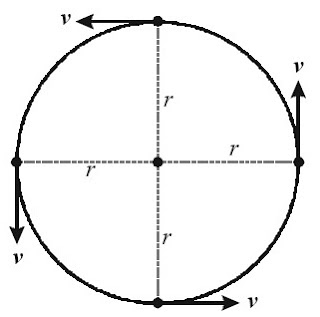 |
| Gambar 1. Arah kecepatan linear dalam gerak melingkar. |
Contoh Soal 1 :
Sebuah benda bergerak melingkar pada sebuah lintasan yang memiliki
diameter 200 cm. Jika benda tersebut berputar sebanyak 1,5 kali putaran,
tentukanlah jarak yang ditempuh benda tersebut.
Kunci Jawaban :
Diketahui: d = 200 cm = 2 m.
Oleh karena jari-jari lingkaran adalah setengah dari panjang diameter maka :
r = ½ × 2 m = 1 m.
Keliling sebuah lingkaran adalah 2π r sehingga jarak yang ditempuh oleh benda tersebut adalah 1,5 kali keliling lingkaran, yakni
Δ s = 1,5 × ( 2π r )
Δ s = 1,5 × 2 × 3,14 × 1 m
Δ s = 9,42 m
Jadi, jarak yang telah ditempuh benda tersebut adalah sejauh 9,42 m.
Waktu yang ditempuh sebuah benda ketika bergerak melingkar dalam satu
putaran penuh disebut periode, yang diberi lambang T dengan satuan
sekon. Banyaknya lintasan yang dapat ditempuh dalam satu sekon disebut
frekuensi, yang diberi lambang f dengan satuan hertz. Nama ini diambil
dari salah seorang ilmuwan yang berjasa dalam ilmu Fisika, yakni Henrich
Hertz (1857–1895). Hubungan antara periode dan frekuensi dapat
dituliskan dalam persamaan berikut.
f = 1 / T (1-2)
Dalam materi gerak lurus, pengertian kecepatan adalah perubahan
perpindahan dalam selang waktu tertentu. Begitu pula dengan gerak
melingkar yang dapat didefinisikan sebagai besarnya panjang lintasan
yang ditempuh dalam selang waktu tertentu. Besarnya kecepatan linear
disebut juga laju linear. Persamaan laju linear dalam gerak melingkar
dapat dituliskan sebagai berikut.
Laju linear = panjang lintasan / selang waktu
atau
v = Δs / Δt
Dalam gerak melingkar, panjang lintasan diubah menjadi keliling lintasan
dan selang waktu yang ditempuh diubah menjadi periode. Oleh karena itu
persamaannya menjadi :
v = 2πr / T (1-3)
Oleh karena 1 / T = f, Persamaan (1–3) dapat ditulis kembali menjadi :
v= 2πrf (1-4)
Contoh Soal 2 :
Sebuah roda yang berjari-jari 50 cm berotasi dengan kecepatan sudut 900
rpm. Kelajuan tangensial sebuah titik pada tepi roda itu adalah ....
a. 7,5π m/s
b. 15π m/s
c. 225 π m/s
d. 350 π m/s
e. 450π m/s
Kunci Jawaban :
Kelajuan tangensial : v= 2πrf = 900 rpm = 900 / 60 sekon = = 15 putaran / sekon
v = 2π × 15 putaran / sekon × 0,5 m
v = 15π m/s
Jawab: b
Contoh Soal 3 :
Sebuah roda sepeda berputar sebanyak 10 kali putaran tiap 1 sekon dengan
kecepatan linear 18 m/s. Tentukanlah panjang diameter roda sepeda
tersebut.
Kunci Jawaban :
Diketahui: f = 10 hertz, dan v = 18 m/s.
Dengan menggunakan Persamaan (1–4), diperoleh :
v = 2πrf
r = v / 2πf
r = 18 m/s / 2 x 3,14 x 10 Hz
r = 0,287 m
Oleh karena jari-jari sebuah lingkaran adalah setengah dari diameter maka :
r = ½ d
d = 2 r
d = 2 × 0,287 m
d = 0,574 m = 5,74 cm
Jadi, diameter roda sepeda tersebut adalah 5,74 cm.
2. Kecepatan Anguler
Perhatikan kembali sebuah benda yang bergerak melingkar seperti pada
Gambar 2. Benda yang bergerak pada lintasannya akan membentuk sudut
tertentu dari posisi awal benda diam. Perubahan sudut ini mengikuti arah
gerak benda pada lintasan tersebut. Perubahan sudut gerak benda akan
bernilai positif jika gerak benda berlawanan dengan arah putaran jam.
Adapun perubahan sudut akan bernilai negatif jika arah gerak benda
searah dengan arah putaran jam.
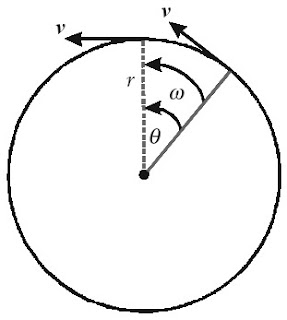 |
| Gambar 2. Arah kecepatan linear dan anguler dengan perubahan sudut θ |
Perubahan sudut dilambangkan dengan Δθ dan memiliki satuan radian.
Biasanya, sering juga satuan perubahan sudut menggunakan derajat.
Hubungan antara radian dan derajat dapat dituliskan sebagai berikut.
1 rad = sudut putaran (dalam derajat) / 2π
Untuk satu putaran penuh,
1 rad = 360° / 2π = 57,3°
Besarnya perubahan sudut ( Δθ ) dalam selang waktu ( Δt ) tertentu
disebut kelajuan anguler atau kelajuan sudut. Kelajuan anguler ini
dilambangkan dengan ω dan memiliki satuan rad/s. Besarnya kelajuan
anguler dapat ditulis sebagai berikut.
Kelajuan anguler = perubahan sudut / selang waktu
atau
ω = Δq / Δt (1-5)
Dalam melakukan satu putaran penuh, sudut yang ditempuh adalah 360° atau
2π rad dalam waktu T sekon, dengan T adalah periode. Dari Persamaan
(1–5), dapat ditulis kembali menjadi :
ω = 2π / T (1-6)
Dari pembahasan sebelumnya, Anda telah mengetahui bahwa frekuensi f = 1 / T sehingga Persamaan (1–6) menjadi
ω= 2πf (1-7)
Contoh Soal 4 :
Sebuah benda yang berada di ujung sebuah CD melakukan gerak melingkar dengan besar sudut yang ditempuh adalah ¾ putaran dalam waktu 1 sekon. Tentukanlah kelajuan sudut dari benda tersebut.
Kunci Jawaban :
Diketahui : f = ¾ / s = 0,75 hertz.
Dengan menggunakan Persamaan (1–7), diperoleh :
ω = 2πf
ω = 2 3,14 0,75 hertz
ω = 4,71 rad/s
Besarnya nilai tersebut menunjukkan nilai kelajuan anguler dalam ¾ putaran.
Jika Anda perhatikan Persamaan (1–6) dan (1–7), terdapat hubungan antara
laju linear (v) dengan kelajuan anguler (ω). Jika persamaan-persamaan
laju linear dan laju anguler ditulis kembali, akan diperoleh persamaan
baru seperti berikut.
v= 2πrf
ω = 2πf
sehingga hubungan antara laju linear (v) dan laju anguler (ω) dapat ditulis menjadi :
v = ω r (1-8)
dengan :
v = laju linear (m/s),
ω = laju anguler (rad/s), dan
r = jari-jari lintasan (m).
Catatan Fisika :
Sudut yang ditempuh oleh sebuah benda untuk bergerak melingkar sama
dengan panjang lintasan (busur) yang dilalui dibagi dengan jari-jari
lintasan θ = s / r
Contoh Soal 5 :
Sebuah partikel bergerak melingkar dengan kelajuan 4 m/s dan jari-jari lintasannya 0,5 m. Tentukanlah kelajuan angulernya.
Kunci Jawaban :
Diketahui:
v = 4 m/s, dan
r = 0,5 m.
Dengan menggunakan Persamaan (1–8), diperoleh :
v = ω r
ω = v / r
ω = (4 m/s) / (0,5 m) = 8 rad/s
B. Percepatan Sentripetal
Pada bab sebelumnya Anda telah belajar mengenai percepatan rata-rata.
Percepatan rata-rata dapat didefinisikan sebagai perubahan kecepatan
dalam selang waktu tertentu. Ketika Anda belajar mengenai gerak lurus
beraturan, percepatan yang dialami sebuah benda sama dengan nol. Apakah
di dalam gerak melingkar beraturan juga berlaku seperti halnya gerak
lurus beraturan? Jawabannya adalah tidak. Mengapa?
Coba Anda perhatikan Gambar 3. Apakah Anda masih mengingat rumus dari
percepatan sesaat pada bab sebelumnya? Percepatan sesaat sebuah benda
dituliskan dalam bentuk limit seperti berikut ini.
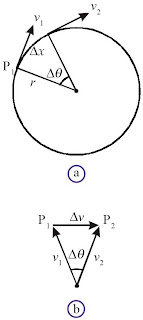 |
| Gambar 3. Vektor kecepatan sebuah benda untuk selang waktu yang sangat kecil, perubahan kecepatan Δv hampir tegak lurus pada v dan mengarah ke pusat lingkaran. |
atau :
Dari persamaan tersebut dapat dilihat bahwa percepatan sesaat (a) searah
dengan perubahan kecepatan (Δv). Jika Δt→0 perubahan kecepatan (Δv)
akan tegak lurus terhadap kecepatan v1 dan v2 sehingga percepatan sesaat
haruslah tegak lurus juga dengan kecepatan v1 dan v2. Jika dibandingkan
sisi pada gambar a dengan gambar b diperoleh :
Jika kedua persamaan (baik di sebelah kiri maupun sebelah kanan) dibagi dengan Δt akan diperoleh :
Pada konsep kecepatan sesaat, nilai percepatan adalah limit dari persamaan tersebut dan jika ditulis ulang akan diperoleh :
dengan menganggap titik P1 semakin dekat dengan P2 maka :
as = v2 / r (1-9)
Percepatan yang tegak lurus terhadap kecepatan yang menyinggung lingkaran ini disebut percepatan sentripetal. Percepatan sentripetal arahnya selalu menuju pusat lingkaran. Jika Anda masih ingat hubungan antara kecepatan linear dan kecepatan sudut, persamaan kecepatan sentripetal dapat ditulis dalam bentuk lain, yaitu
as = ω2r (1-10)
Contoh Soal 6 :
Sebuah bola yang memiliki jari-jari 2 cm berputar dalam bidang lingkaran
horizontal. Satu kali putaran dapat ditempuh bola selama 2 s.
Tentukanlah percepatan sentripetalnya.
Kunci Jawaban :
Diketahui: r = 2 cm = 0,02 m, dan T = 2 s.
v = 2πr / T = 2π (0,02 m) / 2 s = = 0,0628 m/s
as = v2 / r = (0,0628 m/s)2 / 0,02 m
as = 0,917 m/s2
Jadi, percepatan sentripetal yang dialami bola adalah 0,197 m/s2.
C. Gerak Melingkar Beraturan
Pada bab sebelumnya, yakni bab gerak dalam satu dimensi atau disebut
juga sebagai gerak lurus, terdapat gerak lurus beraturan (GLB) dan gerak
lurus berubah beraturan (GLBB) begitu pula dalam gerak melingkar
terdapat gerak melingkar beraturan (GMB) dan gerak melingkar berubah
beraturan (GMBB). Pada bab ini hanya dibahas gerak melingkar beraturan
(GMB), sedangkan gerak melingkar berubah beraturan akan Anda pelajari di
Kelas XI.
Gerak melingkar beraturan (GMB) dapat dianalogikan seperti gerak lurus
beraturan (GLB) di mana kecepatan ω sudut sama dengan kecepatan sesaat.
ω = perpindahan sudut / selang waktu
ω = Δq / Δt
dengan : Δq = Δx / Δr
Jadi,
Oleh karena t0 = 0 maka
ωt = θ − θ0 (1-11)
dan ω = konstan.
Contoh Soal 7 :
Sebuah partikel bergerak melingkar beraturan dengan posisi sudut awal 5
rad. Jika partikel bergerak dengan kecepatan sudut 10 rad/s, tentukanlah
posisi sudut akhir pada saat t = 5 s.
Kunci Jawaban :
Diketahui:
θ0 = 5 rad,
ω = 10 rad/s, dan
t = 5 s.
θ = θ0 + ωt
θ = 5 rad + 10 rad/s × 5 s
θ = 55 rad
Jadi, posisi sudut akhir partikel adalah 55 rad.
Jelajah Fisika :
Helikopter
Helikopter memiliki mesin yang membuat bilahnya berputar beraturan.
Begitu bilah berputar beraturan, mesin mendorong udara ke bawah sehingga
membuat helikopter terangkat ke atas. Dengan memiringkan bilahnya,
pilot dapat membuat helikopter lepas landas, melayang, atau mendarat.
Untuk bergerak maju, bilah harus dimiringkan sehingga bilah mendorong
sebagian udara ke belakang sekaligus ke bawah. Biasanya, helikopter
memiliki rotor kecil di ekornya. Rotor ini dipakai untuk menghentikan
pesawat berputar beraturan ke arah yang berlawanan dari rotor utama.
(Sumber: Oxford Ensiklopedi Pelajar, 1995)
Rangkuman :
1. Sebuah benda dapat dikatakan bergerak melingkar jika lintasan yang dilewatinya berbentuk lingkaran.
2. Kecepatan yang diberikan kepada benda ketika bergerak melingkar, dalam arah tangensial, disebut kecepatan linear.
3. Kecepatan anguler adalah perubahan sudut (Δθ) dalam selang waktu (Δt) tertentu.
4. Hubungan antara kecepatan linear dan kecepatan anguler dapat dituliskan sebagai berikut.
v=ωr
5. Percepatan sentripetal adalah percepatan yang arahnya selalu menuju pusat lingkaran.
6. Gerak melingkar beraturan (GMB) terjadi jika kecepatan anguler benda
bernilai tetap (konstan). Persamaan terdapat dalam GMB adalah :
ω = konstan
θ = θ0 + ωtartikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/01/gerak-melingkar-beraturan-kecepatan-linear-anguler-percepatan-sentripetal.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
No comments:
Post a Comment