1. Syarat Kesetimbangan
Menurut Hukum Pertama Newton, apabila resultan gaya-gaya yang bekerja pada benda sama dengan nol, percepatan benda tersebut juga akan sama dengan nol. Dalam hal ini, dapat diartikan bahwa benda berada dalam keadaan diam atau bergerak dengan kecepatan tetap. Kondisi ini berlaku untuk gerak translasi dan gerak rotasi. Apabila pada benda berlaku hubungan Σ F = 0 dan Στ = 0 (a = 0 dan α = 0) maka dikatakan benda tersebut dalam keadaan setimbang.
Benda yang berada dalam keadaan setimbang tidak harus diam, akan tetapi harus memiliki nilai percepatan linier a = 0 (untuk gerak translasi) dan percepatan sudut α = 0 (untuk gerak rotasi). Sebaliknya, benda yang diam pasti berada dalam keadaan setimbang. Dengan demikian, keadaan setimbang itu terdapat dua macam, yaitu
a. Setimbang statik (benda diam).
v = 0 dan ω = 0
Σ F = 0 dan Στ = 0
b. Setimbang mekanik (benda bergerak translasi atau rotasi).
a. Setimbang translasi → benda bertranslasi dengan v konstan.
b. Setimbang rotasi (untuk benda tegar) → benda berotasi dengan ω konstan.
2. Pusat Massa dan Titik Berat Benda
Benda tegar yang melakukan gerak rotasi, memiliki pusat massa yang tidak melakukan gerak translasi (v = 0). Berbeda dengan sebuah partikel yang bergerak melingkar beraturan, partikel tersebut memiliki pusat massa yang melakukan gerak translasi (v ≠ 0) dengan arah yang selalu berubah karena adanya percepatan sentripetal, as di mana F ≠ 0. Perhatikanlah Gambar 23. berikut.
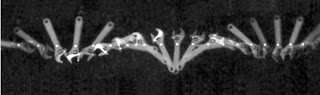 |
| Gambar 23. Pusat massa sebuah kunci Inggris yang sedang berputar berada dalam satu garis lurus. Pusat massa ini bertranslasi dengan arah yang selalu berubah. [4] |
Letak pusat massa suatu benda menentukan kestabilan (kesetimbangan)
benda tersebut. Jika dari titik pusat massa benda ditarik garis lurus ke
bawah dan garis tersebut jatuh pada bagian alas benda, dikatakan benda
berada dalam keadaan setimbang stabil. Namun, apabila garis lurus yang
ditarik dari titik pusat massa jatuh di luar alas benda maka benda
dikatakan tidak stabil.
Menara Pisa yang miring masih tetap dapat berdiri selama berabad-abad. Mengapa menara tersebut tidak jatuh? Dari ilustrasi Gambar 26, dapat dilihat bahwa garis yang ditarik dari pusat massa menara masih jatuh pada alasnya sehingga menara berada dalam keadaan stabil (setimbang).
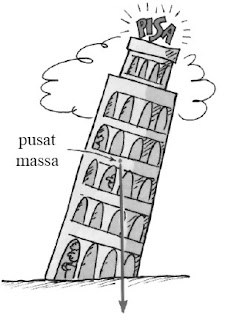 |
| Gambar 24. Letak titik pusat massa menara Pisa masih berada di dalam alasnya sehingga menara tetap dalam keadaan stabil. [4] |
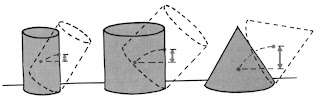 |
| Gambar 25. Benda berbentuk kerucut merupakan benda yang paling stabil dibandingkan dengan ketiga benda lainnya. [4] |
Dari gambar tersebut dapat dilihat bahwa semakin lebar alas suatu benda,
gaya yang dibutuhkan untuk menggulingkannya akan semakin besar karena
jarak yang dibutuhkan untuk menaikkan titik pusat massa benda (ditandai
tanda panah) sehingga benda dapat digulingkan juga besar. Titik berat
benda adalah titik tangkap gaya berat suatu benda, di mana titik
tersebut dipengaruhi oleh medan gravitasi. Penentuan letak titik berat
ini dapat dilakukan dengan mudah apabila benda bersifat homogen dan
beraturan (seperti kubus, bola, dan silinder). Apabila benda tidak
homogen atau tidak beraturan, penentuan titik beratnya adalah sebagai
berikut.
Anggaplah benda berupa kumpulan titik-titik massa, yaitu m1, m2, m3, dan seterusnya yang terletak pada koordinat (x1, y1), (x2, y2), (x3, y3), dan seterusnya. Titik berat benda terhadap sumbu-x adalah (m1 + m2 + m3 + ...) gy0 = m1 gy1 + m2 gy2 + m3 gy3 + ...
Titik berat benda terhadap sumbu-y adalah :
(m1 + m2
+ m3 + ...) gy0 = m1 gy1 + m2
gy2 + m3 gy3 + ...
maka momen gaya berat benda terhadap sumbu-x adalah :
Percobaan Fisika Sederhana 3 :
Menentukan Titik Berat Benda Tidak Beraturan
Alat dan Bahan :
- Sepotong karton dengan bentuk sembarang
- Seutas tali dengan pemberat di ujungnya
- Statif
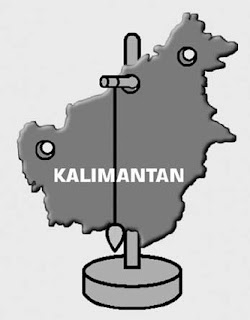
- Buatlah tiga lubang pada potongan karton (letak lubang sembarang) dan berilah nomor lubang 1, lubang 2, dan lubang 3.
- Gantunglah karton itu pada lubang 1 dengan menggunakan statif seperti terlihat pada gambar.
- Gantungkanlah tali yang memiliki pemberat pad statif. Pastikanlah tali dan pemberatnya dapat menggantung secara bebas dan tidak terhalang.
- Setelah karton dan tali berada dalam keadaan setimbang, buatlah garis putus-putus yang berasal dari lubang 1 dan berimpit dengan tali. Kemudian, namai garis itu sebagai garis l1.
- Lakukanlah langkah ke–2 sampai dengan ke-4 pada lubang 2 dan lubang 3.
- Apakah kesimpulan yang Anda dapatkan dari kegiatan tersebut?
- Diskusikan dan komunikasikanlah kesimpulan tersebut dengan teman-teman dan guru Fisika Anda.
Perhatikanlah gambar tiga jenis kesetimbangan statis benda tegar, yaitu
kesetimbangan stabil, labil, dan netral pada Gambar 26. berikut.
 |
| Gambar 26. (a) Benda setimbang stabil (mantap). (b) Benda setimbang labil (goyang). (c) Benda setimbang netral (inde erent/sembarang). |
a. Kesetimbangan stabil (mantap), ialah jenis kesetimbangan benda di
mana apabila benda diberi gangguan (gaya luar) maka benda akan bergerak.
Kemudian, apabila gangguan gaya luar tersebut dihilangkan maka benda
akan diam dan kembali pada kedudukannya semula. Perhatikanlah Gambar
26a. Titik berat benda akan naik, jika benda hendak menggelinding karena
gaya F. Kedudukan benda setelah digulingkan akan tetap.
b. Kesetimbangan labil (goyah), ialah jenis kesetimbangan benda dimana benda tidak dapat kembali ke kedudukannya semula apabila gaya luar (gangguan) yang diberikan padanya dihilangkan. Perhatikanlah Gambar 26b. Titik berat benda O turun, apabila benda hendak menggelinding karena gaya F. Kedudukan benda sebelum dan sesudah digelindingkan berubah.
c. Kesetimbangan netral (indifferent/sembarang), ialah jenis kesetimbangan benda di mana apabila benda diberi gangguan, benda akan bergerak. Kemudian, apabila gangguan dihilangkan, benda akan kembali diam pada posisinya yang baru. Perhatikanlah Gambar 26c. Titik berat benda, O, tidak naik maupun turun apabila benda menggelinding. Setelah menggelinding, benda kembali setimbang di posisinya yang baru.
Catatan Fisika :
Menara Derek
Di kapal dan galangan kapal terdapat derek kapal, yaitu sebuah derek statis yang dioperasikan dengan kabel yang dihubungkan pada sebuah menara. Menara derek juga dapat dijumpai pada pembangunan gedung-gedung. Menara derek ini harus selalu berada dalam keadaan setimbang agar tidak timbul total momen gaya yang akan merobohkan menara derek tersebut.
Salah satu derek yang terkenal adalah derek Gottwald MK 1000 yang diberi julukan “ irdie ne” karena menara derek tersebut pernah mengangkat beban yang sangat berat, yaitu menempatkan reaktor berkapasitas 742 ton di kilang minyak Selandia Baru. (Sumber: Oxford Encyclopedy, 1995)
Contoh Soal 17 :
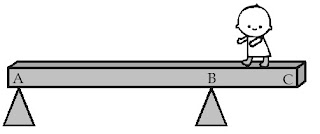
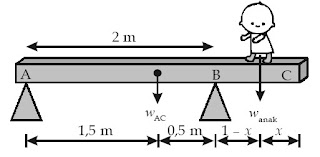
Batang AC bermassa 40 kg dan panjangnya 3 m. Jarak tumpuan A dan B adalah 2 m (di B papan dapat berputar) seorang anak bermassa 25 kg berjalan dari A menuju C. Berapa jarak minimum anak dari titik C agar papan tetap setimbang (ujung batang A hampir terangkat)?
Kunci Jawaban :
Στ = 0
wAC (0,5 m) = wanak (1 – x)
(400 N) (0,5 m) = (250 N)(1 – x)
200 Nm = (250 N) – (250x Nm)
250x Nm = 50 N
x = 0,2 m
Contoh Soal 18 :
Pada sistem kesetimbangan benda tegar seperti pada gambar di samping,
batang AB homogen dengan panjang 80 cm, beratnya 18 N, menyangga beban
seberat 30 N, BC adalah tali.
a. Berapakah tegangan pada tali (dalam newton) jika jarak AC = 60 cm?
b. Tentukanlah besar gaya reaksi dinding terhadap batang di titik A?
Kunci Jawaban :
Diketahui: AB = 80 cm, mAB = 18 N, dan wbeban = 30 N.
Oleh karena AB = 80 cm dan AC = 60 cm maka :
sinα = 0,6 atauα = 37°.
Berdasarkan syarat kesetimbangan gaya pada titik A, diperoleh:
Στ A = 0
T(AD) + FA(0) + (18 N)(1/2 AB) + (30 N)(AB) = 0
T(AB sin 37°) + 0 + (9 N)(AB) + (30 N)(AB) = 0
39 N = 0,6T atau T = 65 N.
Contoh Soal 19 :
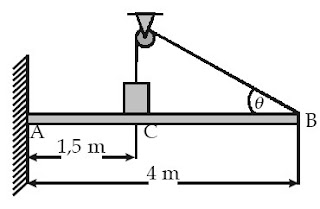
Sistem terlihat pada gambar. Massa batang homogen AB adalah 50 kg dan
massa bebannya 150 kg. Ujung A diengselkan ke tembok, sedangkan beban
dihubungkan ke ujung B dengan seutas tali melalui sebuah katrol. Massa
tali dan gesekan pada katrol diabaikan, g = 10 m/s2, dan sinθ = 7/16 .
a. Gambarkanlah diagram gaya-gaya yang bekerja pada batang AB dan pada beban, serta hitunglah tegangan talinya.
b. Berapakah besar gaya engsel di titik A?
Kunci Jawaban :
Diketahui: m1 = 150 kg, m2 = 50 kg, g = 10 m/s2, AC = 1,5 m, AB = 4 m, dan sinθ = 7/16.
ΣFy = 0
T + NC = m1g
T + NC = 1.500 N
NC = 1.500 N – T …....... (a)
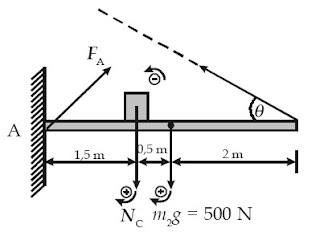
Perhatikanlah diagram gaya pada batang.
Gaya reaksi beban terhadap batang adalah NC' (bukan m1g) dengan NC' = NC (pasangan gaya aksi-reaksi).
Gunakan syarat kesetimbangan batang pada titik A.
ΣτΑ = 0
NC' (AC) + m2g (CB) = T sinθ (AC)
NC' (1,5 m) + m2g (2 m) =
T sinθ (4 m) ........... (b)Substitusikan Persamaan (a) pada Persamaan (b) sehingga diperoleh :
(1.500 N – T)(1,5 m) + (500 N)(2 m) = T (7/16) (4 m)
2.250 Nm – 1,5 T m + 1.000 Nm = 7/4 T m
9.000 Nm – 6 T m + 4.000 Nm = 7T m
13T m = 13.000 Nm → T = 1.000 N.
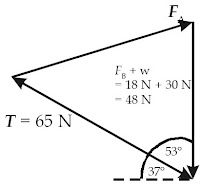
b. Gunakan metoda segitiga untukmenghitung gaya engsel FA.
Contoh Soal 20 :
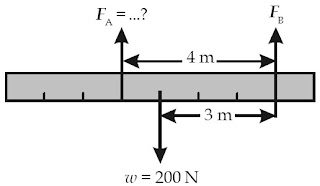
Balok kayu seragam di atas sepanjang 8 m dan berat 200 N berada di atas
dua buah tiang penyangga A dan B. Besar beban yang dirasakan oleh titik A
(dalam N) adalah ....
a. 60
b. 90
c. 120
d. 150
e. 180
ΣτB = 0
w (3 m) – FA (4 m) = 0
(200 N)(3 m) – FA (4 m) = 0
FA = 150 NJawab: d
Benda bidang tersebut dilubangi di lima titik. Kemudian, benda
digantungkan pada paku di dinding. Benda tersebut akan mencapai
keseimbangan indeferen apabila titik berat berada di titik ....
a. P
b. Q
c. R
d. S
e. T
Kunci Jawaban :
Apabila benda berada dalam keseimbangan indeferen (netral), pusat gravitasi benda tetap walaupun benda diberi gaya horizontal. Jadi, pada kasus tersebut benda akan setimbang netral jika pusat massanya di titik R. (Posisi R tetap walaupun benda diputar)
Jawab: c
Contoh Soal 22 :
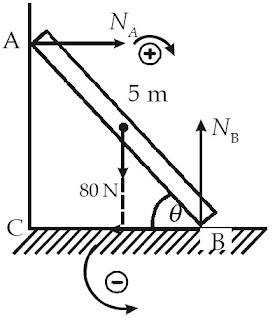
Sebuah tangga homogen AB yang panjangnya 5 m dan massanya 8 kg
disandarkan pada dinding vertikal yang licin. Ujung A bersandar pada
dinding, sedangkan ujung B terletak di lantai kasar yang berjarak 3 m
dari dinding. Tentukan koefisien gesek antara lantai dan ujung B, agar
batang setimbang tepat akan bergerak. (percepatan gravitasi g = 10 m/s2)
Kunci Jawaban :
Diketahui: AB = 5 m, mAB = 8 kg = 80 N, BC = 3 m, AC = 4 m, dan g = 10 m/s2.
ΣτΒ = 0
NA(AC) – WAB (½ CB) = 0
NA(AC) – 80 (½ CB) = 0
NA(4 m) – (40 N)(3
m) = 0 → NA = 30 N
ΣFy = 0 → NB
= 80 N
ΣFx = 0 → fB
= NA atau μNB = NA
μ (80 N) = 30 N → μ= 3/8
3. Kesetimbangan Tiga Gaya
 |
| Gambar 27. Gaya F1, F2, dan F3 bekerja pada titik partikel dengan sudut masing-masing. |
Apabila terdapat tiga gaya yang bekerja pada satu titik partikel dan
partikel tersebut berada dalam keadaan setimbang, seperti pada Gambar
27, berlaku hubungan sebagai berikut.
dengan α 1, α 2, dan α3 merupakan sudut apit antara dua gaya yang berdekatan.
Contoh Soal 23 :
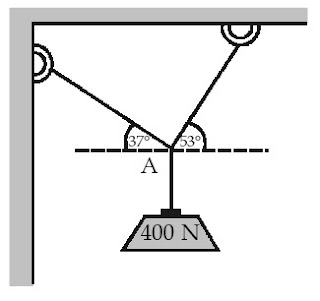
Benda pada gambar memiliki berat 400 N dan digantung dalam keadaan diam.
Tentukanlah besar tegangan-tegangan yang terjadi pada kedua tali yang
menahan benda.
(Ingat, tegangan adalah gaya yang terdapat pada seutas tali yang menarik suatu benda).
(Ingat, tegangan adalah gaya yang terdapat pada seutas tali yang menarik suatu benda).
Kunci Jawaban :
Diketahui: w = 400 N, θ 1 = 37°, dan θ 2 = 53°
Perhatikan diagram uraian gaya yang bekerja pada titik A. Gaya T1 dan T2
menghasilkan komponen-komponen gaya menurut sumbu-x dan sumbu-y yang
diproyeksikan sebagai berikut:
T1x = T1 cos 37° = T1 (0,8) = 0,8 T1
T1y = T1 sin 37° = T1 (0,6) = 0,6 T1
T2x = T2 cos 53° = T2 (0,6) = 0,6 T2
T2y = T2 sin 53°
= T2 (0,8) = 0,8 T2
Terapkan syarat kesetimbangan sehingga diperoleh :
Contoh Soal 24 :
Σ Fx = 0 → T2x – T1x = 0 atau 0,6 T2
– 0,8 T1 = 0
Σ Fx = –0,8 T1
+ 0,6 T2 = 0 ....
(a)
Σ Fy = 0 → T1y – T2y – w = 0 atau
0,6 T1 + 0,8 T2 – 400 = 0
Σ Fy = 0,6 T1 + 0,8 T2 = 400 N .... (b)Contoh Soal 24 :
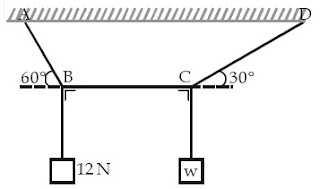
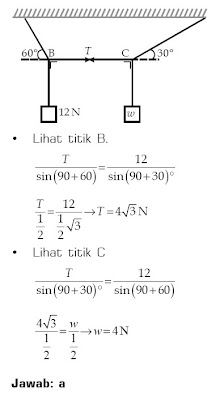
Seutas tali ABCD digantungkan pada titik A dan D. Pada titik B
digantungkan beban seberat w. Tentukanlah besar w agar sistem dalam
kesetimbangan ....
a. 4 N
b. 8 N
c. 12 N
d. 16 N
e. 20 N
4. Kesetimbangan Gaya pada Jembatan
Kesetimbangan statis banyak diaplikasikan dalam bidang teknik, khususnya yang berhubungan dengan desain struktur jembatan. Anda mungkin sering melewati jembatan untuk menyeberangi sungai atau jalan. Menurut Anda, bagaimanakah kesetimbangan statis suatu jembatan jika dijelaskan secara Fisika?
Suatu jembatan sederhana dapat dibuat dari batang pohon atau lempengan batu yang disangga di kedua ujungnya. Sebuah jembatan, walaupun hanya berupa jembatan sederhana, harus cukup kuat menahan berat jembatan itu sendiri, kendaraan, dan orang yang menggunakannya. Jembatan juga harus tahan terhadap pengaruh kondisi lingkungan. Seiring dengan perkembangan jaman dan kemajuan teknologi, dibuatlah jembatan-jembatan yang desain dan konstruksinya lebih panjang dan indah, serta terbuat dari material yang lebih kuat dan ringan, seperti baja. Secara umum, terdapat tiga jenis konstruksi jembatan. Marilah pelajari pembahasan kesetimbangan gaya-gaya yang bekerja pada setiap jenis jembatan berikut.
a. Jembatan kantilever adalah jembatan panjang yang mirip dengan jembatan sederhana yang terbuat dari batang pohon atau lempengan batu, tetapi penyangganya berada di tengah. Pada bagian-bagiannya terdapat kerangka keras dan kaku (terbuat dari besi atau baja). Bagian-bagian kerangka pada jembatan kantilever ini meneruskan beban yang ditanggungnya ke ujung penyangga jembatan melalui kombinasi antara tegangan dan regangan. Tegangan timbul akibat adanya pasangan gaya yang arahnya menuju satu sama lain, sedangkan regangan ditimbulkan oleh pasangan gaya yang arahnya saling berlawanan.
 |
| Gambar 28. Jembatan kantilever ini banyak digunakan di Indonesia untuk menghubungkan wilayah antardaerah. |
Perhatikanlah Gambar 28. Kombinasi antara pasangan gaya yang berupa
regangan dan tegangan, menyebabkan setiap bagian jembatan yang berbentuk
segitiga membagi berat beban jembatan secara sama rata sehingga
meningkatkan perbandingan antara kekuatan terhadap berat jembatan. Pada
umumnya, jembatan kantilever digunakan sebagai penghubung jalan yang
jaraknya tidak terlalu jauh, karena jembatan jenis ini hanya cocok untuk
rentang jarak 200 m sampai dengan 400 m.
b. Jembatan lengkung adalah jembatan yang konstruksinya berbentuk busur
setengah lingkaran dan memiliki struktur ringan dan terbuka. Rentang
maksimum yang dapat dicapai oleh jembatan ini adalah sekitar 900 m. Pada
jembatan lengkung ini, berat jembatan serta beban yang ditanggung oleh
jembatan (dari kendaraan dan orang yang melaluinya) merupakan gaya-gaya
yang saling berpasangan membentuk tekanan. Oleh karena itu, selain
menggunakan baja, jembatan jenis ini dapat menggunakan batuan-batuan
sebagai material pembangunnya. Perhatikanlah Gambar 29. Desain busur
jembatan menghasilkan sebuah gaya yang mengarah ke dalam dan ke luar
pada dasar lengkungan busur.
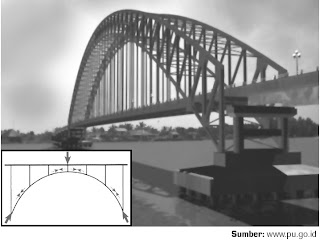 |
| Gambar 29. Salah satu contoh jembatan lengkung adalah jembatan Rumpyang yang terdapat di Kalimantan Selatan. |
c. Jembatan gantung adalah jenis konstruksi jembatan yang menggunakan
kabel-kabel baja sebagai penggantungnya, dan terentang di antara
menara-menara. Setiap ujung kabel-kabel penggantung tersebut ditanamkan
pada jangkar yang tertanam di pinggiran pantai. Perhatikanlah Gambar 30.
Jembatan gantung menyangga bebannya dengan cara menyalurkan beban
tersebut (dalam bentuk tekanan oleh gaya-gaya) melalui kabel-kabel baja
menuju menara penyangga. Kemudian, gaya tekan tersebut diteruskan oleh
menara penyangga ke tanah. Jembatan gantung ini memiliki perbandingan
antara kekuatan terhadap berat jembatan yang paling besar, jika
dibandingkan dengan jenis jembatan lainnya. Oleh karena itu, jembatan
gantung dapat dibuat lebih panjang, seperti Jembatan Akashi-Kaikyo di
Jepang yang memiliki panjang rentang antarmenara 1780 m.
 |
| Gambar 30. Jembatan Ampera yang terdapat di Sumatra Selatan ini menggunakan konstruksi jembatan gantung dengan dua menara. |
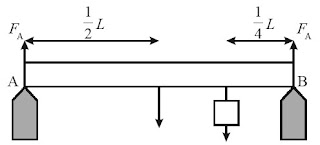
Pada batang homogen seberat 200 N digantungkan beban 440 N dengan
panjang L (lihat gambar). Besar gaya yang dilakukan penyangga pada
batang adalah ....
a. FA = 210 N ; FB = 330 N
b. FA = 430 N ; FB = 210 N
c. FA = 200 N ; FB = 440 N
d. FA = 210 N ; FB = 430 N
e. FA = 440 N ; FB = 200 N
FAL = 200 N (1/2) L + 440 N (1/4) L
FA = 100 N + 110 N
FA = 210 N
Syarat kesetimbangan di titik B adalah Σ = Bτ0.
FBL = 200 N (1/2) L + 440 N (3/4) L
FB = 100 N + 330 N
FB = 430 NJawab: d
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/03/pengertian-gerak-rotasi-kinematika-dan-dinamika-momen-gaya-inersia-kesetimbangan-benda-tegar-contoh-soal-kunci-jawaban.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!

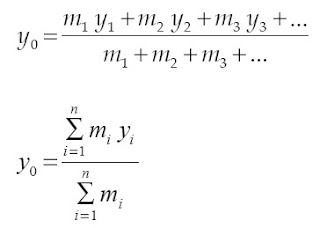









No comments:
Post a Comment