Pada Gambar 1. memperlihatkan sebuah muatan listrik +q' di dalam medan
listrik homogen yang ditimbulkan oleh muatan listrik +q, dipindahkan
dari titik a ke b dengan lintasan Δs.
Untuk memindahkan muatan dari titik a ke b diperlukan usaha (W ). Usaha
yang diperlukan oleh muatan untuk berpindah sepanjang Δs adalah ΔW .
Apabila posisi a adalah ra dan posisi b
adalah rb, besar usaha yang dilakukan dapat dirumuskan sebagai berikut:
 |
| Gambar 1. Muatan q' dipindahkan di dalam medan listrik yang ditimbulkan oleh muatan q. |
Fa adalah (gaya elektrostatis pada titik a)
Fb adalah (gaya elektrostatis pada titik b)
Untuk Δs yang kecil ( Δs mendekati nol) lintasan perpindahan muatan +q'
dapat dianggap lurus, dan gaya elektrostatis rata-rata selama muatan +q'
dipindahkan dapat dinyatakan:
Untuk memindahkan muatan q' dari a ke b tanpa kecepatan, diperlukan gaya
F yang besarnya sama dengan Fc, tetapi arahnya berlawanan.
Apabila arah gaya F terhadap arah perpindahan muatan +q' bersudut α , maka usaha perpindahan muatan +q' dari a ke b adalah:
ΔW = F . Δs .cos α
ΔW = -Fc. Δs .cos α ............................................ (1)
Usaha pemindahan muatan +q' dari a ke b sama dengan beda energi potensial listrik di titik a dan b.
ΔEp = ΔW
ΔEp = -Fc cos α .................................................... (2)
persamaan di atas, besar usaha untuk memindahkan suatu muatan dari titik
a ke titik b dapat ditentukan dengan persamaan berikut ini.
Berdasarkan persamaan (3) diketahui bahwa usaha tidak bergantung pada
panjang lintasan yang ditempuh, tetapi hanya bergantung pada kedudukan
awal dan akhir saja. Medan gaya yang demikian dinamakan medan gaya
konservatif.
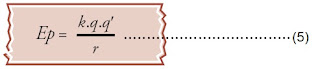
Jika muatan +q' semula pada jarak tak terhingga (∼), besar energi
potensialnya adalah nol. Dengan demikian, apabila muatan +q' dipindahkan
dari tempat yang jauh tak terhingga ke suatu titik b, besar usahanya
adalah sebagai berikut:
Jadi, untuk sembarang titik, besar energi potensialnya dirumuskan:
dengan:
Ep = energi potensial listrik (J)
r = jarak antara +q dan -q (m)
q,q' = muatan listrik (C)
k =
konstanta pembanding (9 × 109 Nm2/C2)
Contoh Soal 1 :
Sebuah muatan listrik dipindahkan dalam medan listrik homogen dengan gaya sebesar  sejauh 20 cm. Jika arah gaya bersudut 30o terhadap perpindahan muatan listrik, berapa beda potensial listrik tempat kedudukan awal dan akhir muatan listrik tersebut?
sejauh 20 cm. Jika arah gaya bersudut 30o terhadap perpindahan muatan listrik, berapa beda potensial listrik tempat kedudukan awal dan akhir muatan listrik tersebut?
Penyelesaian:
Diketahui:
F = 
Δs = 20 cm = 2 × 10-1 m
α =
30o
Ditanya: ΔEp = ... ?
Contoh Soal 2 :
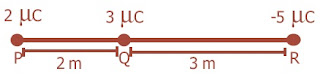
Titik P, Q, dan R terletak pada satu garis dengan PQ = 2 m dan QR = 3 m.
Pada masing-masing titik terdapat muatan 2 μC, 3 μC, dan -5 μC.
Tentukan besarnya energi potensial muatan di Q!
Penyelesaian:
Diketahui:
PQ = 2 m
QR = 3 m
qP = 2 μC = 2 × 10-6 C
qQ = 3 μC = 3 × 10-6 C
qR
= -5 μC = -5 ×
10-6 C
Ditanya: EpQ = ...?
Ep di Q = Ep1 + Ep2 (karena besaran
skalar)
EpQ
= (27 × 10-3) + (45 × 10-3) = 72 × 10-3 J = 7,2 × 10-2 J2. Potensial Listrik
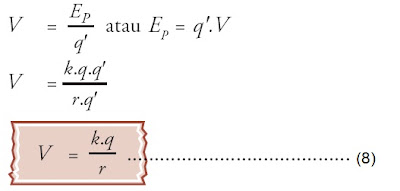
Potensial listrik yaitu energi potensial tiap satu satuan muatan positif.
Potensial listrik termasuk besaran skalar, dan secara matematis dapat dirumuskan:
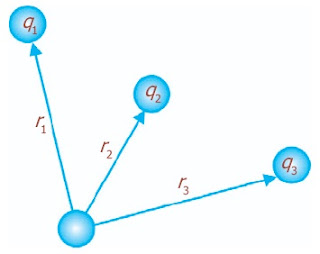 |
| Gambar 2. Potensial listrik bergantung pada muatan q1, q2, dan q3.. |
V = Ep / q .......................................................... (6)
Beda potensial kadang-kadang ditulis dengan persamaan ΔV = V1 – V2,
untuk selanjutnya hanya ditulis V saja. Sesuai dengan batasan di atas,
potensial listrik suatu titik sejauh r dari muatan q besarnya dapat
dinyatakan sebagai berikut:
dengan:
V = potensial listrik (volt)
q = muatan listrik (coulomb)
r = jarak (meter)
Jika terdiri atas beberapa muatan sumber, besarnya potensial listrik
adalah jumlah aljabar biasa dari masing-masing potensial. Misalnya,
kumpulan muatan sumber adalah q1, q2, dan q3, maka potensial listrik pada titik P adalah:
dengan r1 adalah jarak
antara q1 ke P, r2 adalah jarak q2 ke P, dan r3
adalah jarak q3 ke P. Potensial listrik merupakan
besaran skalar, sehingga dalam memasukkan tanda positif atau negatif
pada muatan harus dengan benar.
Contoh Soal 3 :
Bola kecil bermuatan +2 μC , -2 μC , 3 μC , dan -6 μC diletakkan di
titik-titik sudut sebuah persegi yang mempunyai panjang diagonal 0,2 m.
Hitung potensial listrik di titik pusat persegi!
Penyelesaian:
Diketahui:
q1 = +2 μC = 2 × 10-6 C
q2
= -2 μC = -2 × 10-6 C q3= 3 μC = 3 × 10-6 C
q4 = -6 μC = -6 × 10-6 C
Panjang diagonal = 2 × 10-1 m, sehingga jarak tiap-tiap muatan dari titik pusat
r1 = r2 = r3 = r4
= ½ (2×10-1)
r = 10-1 m
3. Potensial Listrik oleh Bola Konduktor Bermuatan
Potensial listrik di sekitar atau di dalam bola konduktor bermuatan
dapat ditentukan dengan cara menganggap muatan bola berada di pusat
bola.
Selanjutnya, potensial listrik di titik-titik pada suatu bola bermuatan,
seperti diperlihatkan pada gambar di samping dapat ditentukan melalui
persamaan (8), yaitu:
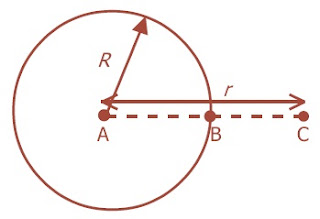 |
| Gambar 3. Potensial listrik pada bola konduktor bermuatan. |
Dari persamaan-persamaan di atas dapat disimpulkan bahwa potensial
listrik di dalam bola sama dengan di permukaan bola, sehingga:
4. Potensial Listrik pada Keping Sejajar
Dua keping sejajar seluas A terpisah dengan jarak d masing-masing diberi muatan +q dan -q.
Rapat muatan listrik σ didefinisikan sebagai muatan listrik per satuan luas.
 |
| Gambar 4. Potensial listrik pada keping sejajar. |
σ = q / A
Potensial listrik:
- di antara dua keping
V = E.r .............................................................. (12)
- di luar keping
V = E.d .............................................................. (13)
artikel ini disalin lengkap dari: http://perpustakaancyber.blogspot.co.id/2013/04/pengertian-energi-potensial-listrik-rumus-contoh-soal-bola-konduktor-bermuatan-keping-sejajar-jawaban-fisika.html
halaman utama website: http://perpustakaancyber.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!



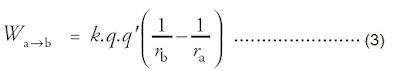
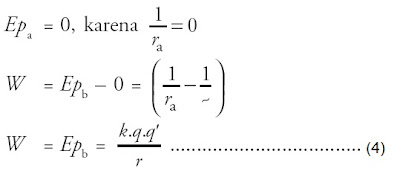
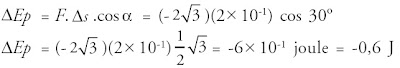


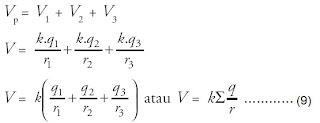

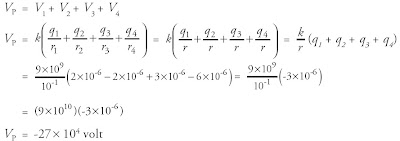
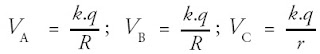

No comments:
Post a Comment