Melukis lingkaran dari Segitiga

Lingkaran luar segitiga merupakan lingkaran yang melalui ketiga titik sudut segitiga.

Bagaimana cara menentukan titik pusat dari lingkaran luar segitiga? Titik pusat lingkaran luar segitiga merupakan perpotongan dari garis sumbu masing-masing sisi segitiga tersebut.

• Melukis Lingkaran Luar Segitiga

Untuk melukis lingkaran luar segitiga kita membutuhkan jangka. Langkah-langkahnya adalah sebagai berikut.

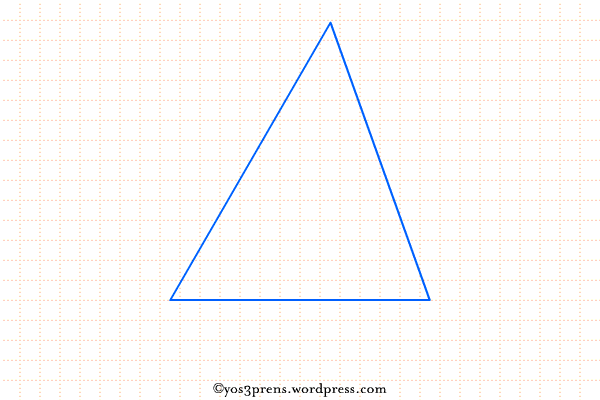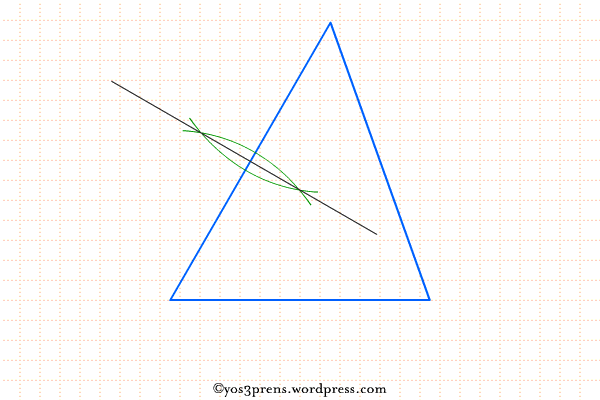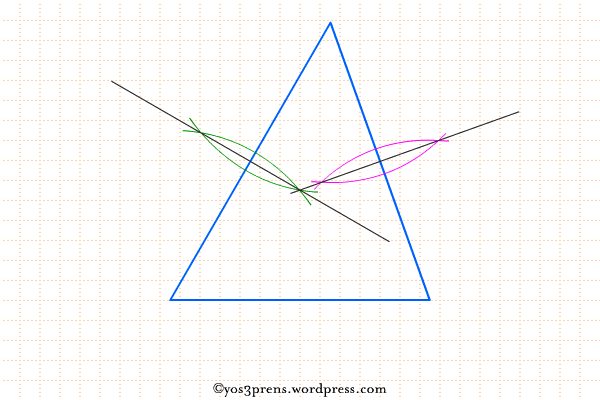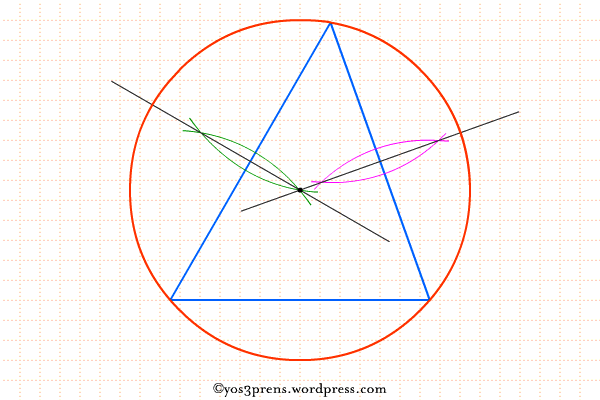
1. Lukislah garis sumbu dari salah satu sisi segitiga. Garis sumbu merupakan garis yang tegak lurus dan membagi sisi segitiga menjadi dua bagian yang sama panjang.
2. Lukis garis sumbu pada sisi lain segitiga. Garis sumbu kedua ini akan memotong garis sumbu yang dihasilkan pada langkah 1.
   
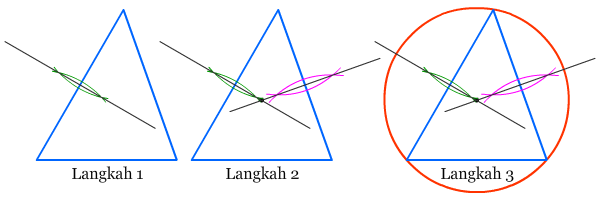
3. Titik potong kedua garis sumbu merupakan titik pusat dari lingkaran luar segitiga. Aturlah jangka sedemikian sehingga pusatnya ada di titik pusat lingkaran luar dan bagian lainnya pada salah satu titik sudut segitiga. Kemudian dengan pengaturan seperti itu buatlah lingkaran penuh.

Lingkaran yang dihasilkan pada langkah-langkah di atas merupakan lingkaran luar dari segitiga yang diberikan. Untuk lebih memahami dalam melukis lingkaran luar segitiga, perhatikan ilustrasi berikut.

Setelah kita dapat melukis lingkaran luar segitiga, selanjutnya kita akan menentukan jari-jari dari lingkaran tersebut.

• Menentukan Jari-jari Lingkaran Luar Segitiga

Untuk menentukan jari-jari lingkaran luar segitiga, kita harus mengetahui panjang dari semua sisi segitiga tersebut. Misalkan a, b, dan c adalah panjang sisi-sisi segitiga ABC, dan t adalah tinggi dari segitiga tersebut.

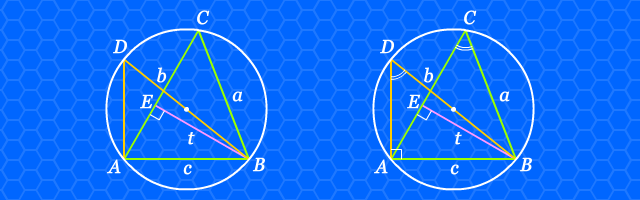
Pertama, lukislah ruas garis yang melalui salah satu titik sudut segitiga dan titik pusat lingkaran. Misalkan ruas garis tersebut adalah ruas garis BD. Selanjutnya dari ujung ruas garis tersebut yang bukan titik sudut segitiga, yaitu titik B, tariklah ruas garis ke titik sudut segitiga yang lain. Misalkan kita tarik ruas garis dari titik B ke titik sudut A, sehingga terbentuk ruas garis AD.
Sudut-sudut ADB dan ACB merupakan sudut keliling yang menghadap busur yang sama, sehingga kedua sudut tersebut kongruen. Sedangkan sudut BAD menghadap diameter, sehingga sudut tersebut memiliki besar 90° atau merupakan sudut siku-siku. Dengan menggunakan prinsip sudut, sudut (sd, sd), kita dapat memperoleh bahwa segitiga BAD sebangun dengan segitiga BEC. Sehingga dengan menggunakan aturan kesebangunan,

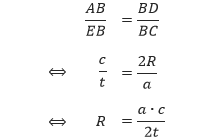
Perhatikan bahwa luas segitiga ABC dapat ditentukan dengan menggunakan rumus L = (b ∙ t)/2. Atau dengan kata lain, t = 2L/b. Sehingga,

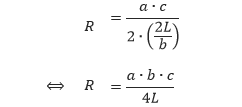
Apabila segitiga diketahui panjang ketiga sisinya, maka kita dapat menentukan luas segitiga tersebut dengan rumus, L = √[s ∙ (s – a)(s – b)(s – c)], dengan s adalah setengah dari keliling segitiga, s = (a + b + c)/2. Sehingga,

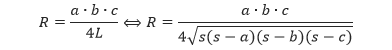
• Melukis Lingkaran Dalam Segitiga

Lingkaran dalam segitiga adalah lingkaran yang menyinggung semua sisi dari suatu segitiga. Sehingga sisi-sisi segitiga tersebut tegak lurus dengan jari-jari lingkaran. Perhatikan gambar berikut!

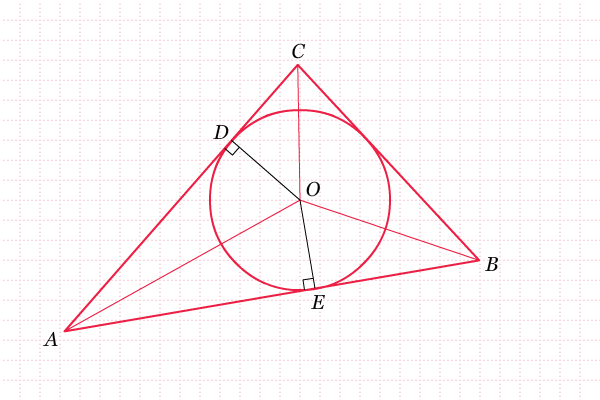
Lingkaran O adalah lingkaran dalam dari segitiga ABC. Sekarang perhatikan bahwa EO = DO dan OA = OA, sehingga segitiga AEO dan segitiga ADO merupakan segitiga-segitiga yang kongruen. Sehingga sudut-sudut yang bersesuaian, yaitu sudut OAE dan sudut OAD sama besar. Oleh karena itu, garis AO merupakan garis bagi sudut DAE.
Dari uraian di atas, titik pusat lingkaran dalam segitiga merupakan perpotongan dari garis-garis bagi dari semua sudut segitiga tersebut. Berikut ini langkah-langkah dalam melukis lingkaran dalam segitiga.

1. Lukislah garis bagi dari dua sudut dalam segitiga. Titik perpotongan garis-garis bagi tersebut merupakan titik pusat dari lingkaran dalam segitiga tersebut.
2. Dari titik pusat tersebut, buatlah garis yang tegak lurus dengan salah satu sisi segitiga.
   
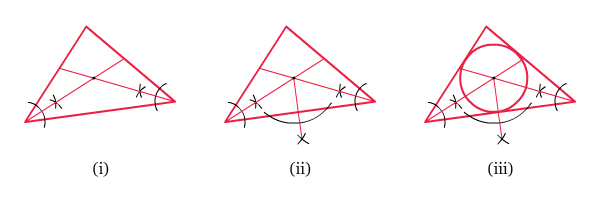
3. Dan selanjutnya, lukislah lingkaran yang berpusat di titik yang diperoleh pada langkah 1 dan melalui titik perpotongan antara garis yang diperoleh pada poin 2 dan sisi segitiga yang tegak lurus dengan garis tersebut.

Agar lebih memahami dalam melukis lingkaran dalam segitiga, perhatikan ilustrasi berikut ini.

• Menentukan Jari-Jari Lingkaran Dalam Segitiga

Lingkaran dalam segitiga merupakan lingkaran yang memiliki titik pusat di perpotongan garis bagi dari ketiga sisi suatu segitiga. Sifat dari lingkaran dalam segitiga adalah bahwa lingkaran tersebut memotong masing-masing sisi segitiga tepat pada satu titik potong.

Pada pembahasan sebelumnya, kita telah berlatih untuk melukis lingkaran dalam dari suatu segitiga. Lalu, bagaimana kita dapat menentukan panjang jari-jari lingkaran dalam tersebut? Untuk menjawab pertanyaan tersebut, perhatikan permasalahan mengenai lingkaran dalam segitiga berikut :

Pak Hasan membangun tokonya tepat di tengah-tengah 3 jalan yang membentuk segitiga, sehingga jarak antara toko tersebut dengan ketiga jalan yang mengelilinginya adalah sama. Panjang ketiga jalan yang mengelilingi toko Pak Hasan tersebut secara berturut-turut adalah 500 meter, 600 meter, dan 800 meter.

Dari permasalahan di atas, dapatkah kita menentukan jarak antara toko Pak Hasan dengan ketiga jalan yang mengelilinginya? Untuk menjawab pertanyaan tersebut, perhatikan bahwa toko Pak Hasan memiliki jarak yang sama dengan ketiga jalan yang mengelilinginya. Kita dapat menduga bahwa toko Pak Hasan merupakan titik pusat dari lingkaran yang memotong ketiga jalan tersebut tepat di satu titik. Atau dengan kata lain, toko Pak Hasan merupakan titik pusat dari lingkaran dalam segitiga yang dibentuk oleh ketiga jalan yang mengelilinginya. Untuk lebih jelasnya perhatikan gambar berikut.

Untuk menentukan jarak antara toko Pak Hasan dengan ketiga jalan yang mengelilinginya, sama saja dengan menentukan jari-jari lingkaran dalam yang terlihat pada gambar di atas.

1. Menemukan Rumus Jari-jari Lingkaran Dalam Segitiga

Diberikan suatu segitiga yang panjang ketiga sisinya adalah a, b, dan c. Untuk menentukan jari-jari lingkaran dalam segitiga tersebut, perhatikan gambar berikut.

Luas dari segitiga paling kanan dapat ditentukan dengan dua cara. Cara pertama dengan menggunakan rumus.
L = √[s(s – a)(s – b)(s – c)] dengan s adalah setengah keliling segitiga atau s = (a + b + c)/2. cara kedua adalah dengan menjumlahkan daerah warna orange, hijau, dan biru. Luas daerah warna orange adalah (a × r)/2, luas daerah warna hijau adalah (b × r)/2, sedangkan luas daerah warna biru adalah (c × r)/2. Sehingga,

Sehingga, untuk sembarang segitiga yang memiliki panjang sisi a, b, dan c, serta s adalah setengah dari kelilingnya, maka jari-jari lingkaran dalamnya dapat ditentukan sebagai berikut.

Dengan rumus di atas, kita dapat menentukan jarak antara toko Pak Hasan dengan ketiga jalan yang mengelilinginya. Karena panjang ketiga jalan yang mengelilinginya secara berturut-turut adalah 500 meter, 600 meter dan 800 meter, maka s = (500 + 600 + 800)/2 = 950. Sehingga jaraknya dapat ditentukan sebagai berikut.

Jadi, jarak antara toko Pak Hasan dengan ketiga jalan yang mengelilinginya adalah 157,7 meter. Seperti itulah cara untuk menentukan jari-jari lingkaran dalam segitiga

artikel ini disalin lengkap dari: https://indritewe.wordpress.com/2013/10/16/lingkaran-luar-dan-dalam-segitiga/
halaman utama website: https://indritewe.wordpress.com/
Jika ada waktu, Dimohon untuk Membuka Halaman Utama website yang telah saya salin artikelnya ya!