Kata kinematika dikemukakan oleh fisikawan Prancis yang bernama A.M. Ampere
cinematique yang diadopsi dari Yunani kuno κίνημα (re : kinema atau gerak). Kinematika
merupakan cabang ilmu mekanika kalsik yang mempelajari gerakan benda dan
sistemnya tanpa mempermasalahkan gaya penyebab gerakan. Kebalikan dari
kinematika adalah dinamika atau kinetika yang mempelajari gerakan benda dan
mempermasalahkan gaya yang mempengaruhi gerakannya. Biasanya, studi mengenai
kinematika disebut sebagai geometri gerak.
Kinematika gerak benda mempelajari karakteristik gerak suatu partikel yang
diposisikan sebagai vektor. Kinematika gerak ini berhubungan sangat erat dengan
pengaplikasian vektor dalam pembahasannya. Seperti kecepatan, kelajuan, posisi,
gerak relatif, gerakan kordinat dll. Untuk lebih memahami tentang analisis
vektor ini, mari kita simak di poin berikutnya.
2. ANALISIS
VEKTOR
Besaran yang mempunyai besar dan arah disebut dengan vektor. Sementara
besaran yang hanya memiliki besar saja seperti massa dan waktu disebut skalar.
Notasi vektor dan teknik-teknik dengan menggunakan analisis vektor sangat
berguna untuk menjelaskan hukum-hukum
fisika dan aplikasinya baik dalam bidang maupun ruang. Vektor biasa digambarkan
sebagai segmen atau ruas garis yang berarah atau dengan sebuah anak panah
sebagai berikut:
Dalam vektor terdapat dua komponen utama, yaitu komponen
horizontal (sumbu x) dan komponen vertikal (sumbu y). Kedua komponen vektor
tersebut memiliki resultan yang memiliki arah yang merupakan akar dari jumlah
kuadrat komponen x dan y. Cara menentukan komponen-komponen vektor:
Besar vektor ditentukan dengan panjang dari anak
panah, menggunakan satuan yang tepat (sesuai).
Ada tiga jenis vektor :
- Vektor Bebas (free vector), vektor ini merupakan vektor yang bisa digeser sejajar dirinya dengan panjang dan arah yang tetap.
- Vektor meluncur (sliding vector), vektor yang bisa digeser sepanjang garis kerjanya, misalnya gaya yang bekerja sepanjang garis lurus.
- Vektor terikat (binding vector), vektor ini merupakan vektor yang terikat pada sistem koordinat yang menunjukkan posisi tertentu.
PENGOPERASIAN
VEKTOR
a. Penjumlahan vektor secara geometris
Dibawah ini
terdapat 3 vektor yaitu :
Dari ketiga
vektor tersebut, dapat dijumlahkan dengan cara:
b. Pengurangan vektor secara
geometris
Pengurangan vektor dapat dilakukan dengan menjumlahkan vektor 1 dengan
lawan vektor 2
c. Penjumlahan dan pengurangan
vektor secara analisis
Untuk menjumlahkan vektor 3 dimensi, digunakan cara analisis:
Vektor
dapat diuraikan menjadi Ax dan Ay
Ax = a cos
θ
Ay = a cos
θ
Untuk
menentukan besar dan arahnya digunakan rumus:
d. Perkalian Vektor
Perkalian vektor dengan hasil akhirnya berupa skalar. Operasi ini disebut
juga “dot product”
Jika dua buah vektor dikalikan dengan hasil akhirnya vektor lain, maka
rumus diatas hanya diganti menjadi sin. Cara ini disebut “cross product”
Arah dari hasilperkalian vector a dan b selalu tegak lurus dengan bidang
yang dibentuk oleh vektor a dan b.
3. HUBUNGAN
KINEMATIKA DENGAN ANALISIS VEKTOR
Dari penjelasan di atas, penggunaan vektor dalam ilmu kinematika dapat
dilihat dalam pembahasan posisi dan perpindahan partikel, kecepatan partikel,
percepatan partikel, gerak lurus dan melingkar.
a. Posisi dan Perpindahan
Partikel
Posisi merupakan
kedudukan benda terhadap titik acuan. Posisi dapat dinyatakan dengan
vektor-vektor satuan, pada sumbu x ditulis i, dan sumbu y ditulis j.
Perpindahan
adalah perubahan posisi benda dalam waktu tertentu. Perpindahan dapat
dirumuskan:
Dengan arah
perpindahan :
Grafik
perpindahan dalam berbagai macam grafik terhadap kecepatan dan waktu :
b. Kecepatan Partikel
Kecepatan rata-rata adalah hasil bagi perpindahan dengan waktu tempuhnya.
Dengan
arah kecepatan:
Kecepatan
sesaat adalah kecepatan rata-rata untuk Δt mendekati nol.
Kecepatan
sesaat dapat dilihat dengan pendekatan grafik :
Kecepatan
sesaat merupakan turunan pertama fungsi posisi
Posisi
partikel dapat ditentukan menggunakan integral dari fungsi kecepatan
Lalu
dapat dicari resultannya, atau :
c. Percepatan Partikel
Percepatan rata-rata adalah perubahan kecepatan dalam waktu tertentu.
Dengan
arah percepatan:
Percepatan
sesaat adalah kecepatan rata-rata untuk Δt mendekati nol
Percepatan
sesaat merupakan turunan pertama fungsi kecepatan dan turunan kedua fungsi
posisi.
Kecepatan
dapat ditentukan menggunakan integral dari fungsi percepatan
Lalu
dapat dicari resultannya.
d.
Gerak Lurus dan melingkar
Gerak Lurus adalah gerak yang dipengaruhi oleh kecepatan linear, sedangkan
gerak melingkar dipengaruhi oleh kecepatan sudut. Hubungan GLBB dengan GMBB
dengan analisis vektor:
Gerak melingkar berubah beraturan dipengaruhi oleh :
- Kecepatan linear
- Kecepatan angular/sudut
- Percepatan tangensial/linear
- Percepatan sentripetal
Kecepatan linear pada GMBB arahnya menuju arah gerak benda (lurus) yaitu
menyinggung lintasan gerakan, dimana lintasannya berupa busur/ keliling
lingkaran. Dapat dirumuskan:
Kecepatan
angular/sudut pada GMBB arahnya menuju arah putaran benda (melingkar) yaitu
berupa perubahan besar sudut busur lingkaran. Dapat dirumuskan:
Percepatan
tangensial/linear pada GMBB :
- Arahnya searah dengan garis singgung lingkaran.
- Arahnya sejajar dengan kecepatan linear
- Arah tegak lurus dengan percepatan sentripetal
- Mengubah besar kecepatan total benda.
Dapat dirumuskan
:
Percepatan
sentripetal pada GMB :
- Arahnya menuju pusat lingkaran
- Arahnya tegak lurus dengan percepatan tangensial.
- Mengubah arah kecepatan total benda (menuju pusat).
Dapat dirumuskan:
Menghasilkan
gaya sentripetal:
Percepatan total
adalah perpaduan antara percepatan tangensial dan percepatan sentripetal, dapat
dirumuskan:
Dengan arah
percepatan total:
artikel ini disalin lengkap dari: http://softilmu.blogspot.co.id/2015/12/Hubungan-Kinematika-Gerak-dengan-Analisa-Vektor.html
halaman utama website: http://softilmu.blogspot.co.id/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!




















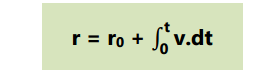














No comments:
Post a Comment