Bidang-bidang yang hanya mempunyai
panjang dan lebar tetapi tidak mempunyai tinggi disebut bidang dimensi
dua atau bidang datar. Begitu juga bidang-bidang yang hanya mempunyai
panjang dan tidak mempunyai lebar dan tinggi disebut bidang dimensi satu
atau bidang garis.
A. Titik
Secara matematik definisi titik adalah sesuatu yang tidak mempunyai bagian sama sekali, tidak berbentuk dan tidak mempunyai ukuran.
Dari pengertian di atas, maka titik dapat dijabarkan sebagai berikut:
1. Tidak mempunyai ukuran
2. Tidak memeiliki panjang, lebar atua tebal.
3. Memiliki tempat (posisi)
4. Tidak dapat dilihat
Titik adalah bagian terkecil dari suatu objek geometri, yang menempati suatu tempat, yang tidak memiliki panjang, lebar, dan tinggi.Titik adalah suatu idea, benda pikiran yang bersifat abstrak. Dikarenakan titik tidak bisa dijelaskan dengan cara biasa, Titik termasuk sesuatu yang tak terdefinisi.
Berdasarkan penjabaran di atas, maka untuk menandai sebuah titik dapat disimbolkan dalam wujud noktah atau silang:
1. “.” Noktah untuk mewujudkan titik.
2. “x” Silang untuk mewujudkan titik.
Ingat! Nama sebuah titik menggunakan huruf kapital. Contohnya: A
B. Garis
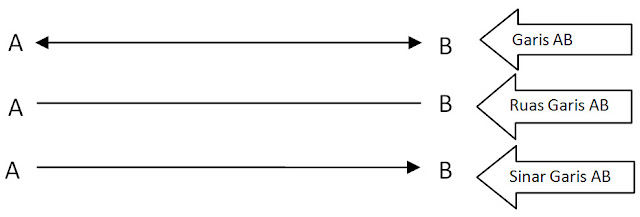
Garis adalah himpunan dari titik-titik yang mempunyai panjang tak terhingga tetapi tidak memiliki lebar atau tebal.Panjangnya tak terbatas, lurus, tidak mempunyai ketebalan, dan tidak mempunyai ujung.
Gambar diatas untuk menunjukkan sebuah garis, dan penjelasannya sebagai berikut:
Melalui dua buah titik A dan B dapat digambar sebuah garis AB dan ditulis AB. Karena sifatnya tidak terbatas atau tidak terhingga, maka gambar (model) garis diberi panah pada kedua ujungnya.
Ciri-ciri garis yaitu:
1. Tidak mempunyai pangkal.
2. Tidak mempunyai ujung.
3. Panjangnya tak terhingga.
Titik yang terletak pada satu garis yang sama disebut titik-titik segaris (kolinear). Misalnya titik-titik A dan B yang terletak pada satu garis:
Dua garis disebut sejajar, jika keduanya tidak saling berpotongan atau berimpit. Jadi dapat dikatakan bahwa satu garis adalah sejajar dengan dirinya sendiri.
Tiga atau lebih garis yang melalui satu titik yang sama disebut garis setitik atau garis yang kongruen.
Ruas garis digambarkan diatas penjelasanya sebagai berikut:
Disebut ruas garis AB ditulis AB (tidak dengan panah). Ruas garis AB adalah himpunan titik-titik A dan B dan semua titik-titik diantara A dan B. Ciri-ciri ruas garis yaitu:
1. Mempunyai pangkal.
2. Mempunyai ujung.
3. Panjangnya terhingga (terbatas/dapat diukur).
Sinar garis digambarkan diatas, penjelasannya sebagai berikut:
Disebut sinar garis AB ditulis AB .Sinar AB adalah himpunan bagian dari garis termasuk titik A dan semua titik di sisi/ di pihak yang sama. Ciri-ciri sinar garis yaitu:
1. Mempunyai pangkal.
2. Tidak mempunyai ujung (digambar panah).
3. Panjangnya tidak terhingga.
C. Sudut
Sudut dibentuk oleh dua garis lurus yang berpotongan pada satu titik yang sisi-sisinya bersekutu pada salah satu ujungnya. Ciri-cirinya yaitu sisi-sisi sudut dibentuk oleh ruas-ruas garis dan sudut terbentuk karena ruas-ruas garis yang pangkalnya bersekutu (bertemu) pada satu titik yang disebut titik sudut.
Berdasarkan besar sudutnya, maka sudut digolongkan menjadi empat jenis, yaitu:
1. Sudut lurus adalah sudut yang besarnya 180o.
2. Sudut siku adalah sudut yang besarnya 90o.
3. Sudut lancip adalah sudut yang besarnya antara 0o – 90o.
4. Sudut tumpul adalah sudut yang besarnya lebih dari 90o.
D. Bidang
Bidang adalah permukaan rata yang meluas ke segala arah,tak terbatas, terus-menerus dalam semua arah, dan tidak memiliki ketebalan.Bidang adalah himpunan titik-titik yang memiliki luas tak terhingga.Bidang terdiri dari bidang datar dan bidang ruang.
Bidang datar disebut juga bidang berdimensi dua karena hanya mengandung unsur panjang dan lebar.Berikut ini merupakan macam-macam bidang datar, yaitu:
1. Segitiga
Segitiga adalah gabungan dari tiga segmen/ruas garis yang titik-titiknya tidak kolinier (tidak terletak pada satu garis). Ditinjau dari besar sudutnya, segitiga digolongkan menjadi:
a. Segitiga lancip (ketiga sudutnya lancip).
b. Segitiga siku-siku (salah satu sudutnya 90o).
c. Segitiga tumpul (salah satu sudutnya tumpul, >90o).
Sedangkan ditinjau dari panjang sisinya, segitiga digolongkan menjadi:
a. Segitiga sama sisi yang ketiga sisinya sama panjang.
b. Segitiga sama kaki yang mempunyai dua sisi yang sama panjang.
c. Segitiga sembarang yang ketiga sisinya tidak sama panjang.
Secara umum, sifat-sifat segitiga adalah sebagai berikut:
a. Mempunyai tiga sisi yang ketiga ujungnya saling bertemu dan membentuk tiga sudut.
b. Mempunyai tiga buah titik sudut.
c. Ketiga sudut besarnya 180o.
2. Segi Empat
Segi empat adalah suatu bangun yang mempunyai 4 sisi dan 4 sudut. Segi empat digolongkan menjadi:
a. Persegi (bujur sangkar), adalah bidang datar yang semua sisinya sama panjang dan keempat sudutnya siku-siku.
Sifat-sifat persegi yaitu:
- Jumlah sudut dalamnya 360o.
- Keempat sudutnya siku-siku.
- Sisi-sisinya sama panjang.
- Diagonalnya sama panjang.
- Perpotongan diagonalnya membentuk sudut 90o atau saling tegak lurus.
- Tiap-tiap sudut dibagi oleh diagonal menjadi dua bagian sama besar.
b. Persegi panjang, adalah segi empat yang keempat sudutnya siku-siku danmempunyai sisi berhadapan yang sama panjang. Sifat-sifat persegi panjang yaitu:
- Setiap sudutnya siku-siku.
- Sisi-sisi yang berhadapan sama panjang.
- Jumlah sudut dalamnya 360o.
- Kedua diagonalnya berpotongan di tengah.
c. Jajar genjang, adalah bidang datar bersegi empat, sisi-sisi yang berhadapan sama panjang dan sejajar. Sifat-sifat jajar genjang yaitu:
- Jumlah sudut dalamnya 360o.
- Sudut-sudut yang berhadapan sama besar.
- Sisi-sisi yang berhadapan sama panjang.
- Diagonal yang satu membagi diagonal yang lain menjadi dua bagian yang sama panjang.
d. Belah ketupat, dapat disebut juga jajar genjang yang keempat sisinya sama panjang. Sifat-sifat belah ketupat yaitu:
- Jumlah sudut dalamnya 360o.
- Sudut-sudut yang berhadapan sama besar.
- Sisi-sisinya sama panjang.
- Diagonalnya saling berpotongan dan saling tegak lurus (membentuk sudut 90o).
- Tiap-tiap sudut dibagi oleh diagonal menjadi dua sama besar.
e. Trapesium, adalah segi empat yang dua sisinya sejajar. Ada 3 jenis trapesium, yaitu trapesium yang keempat sisinya tidak sama panjang, trapesium sama kaki yang kedua sisi tegaknya sama panjang, dan trapesium siku-siku yang salah satu sudutnya siku-siku. Salah satu sifat trapesium yaitu dua sisinya sejajar.
f. Layang-layang, adalah segi empat yang kedua pasang sisinya saling berdekatan sama panjang dan salah satu diagonalnya memotong tegak lurus sumbu diagonal lainnya. Sifat-sifatnya yaitu:
- Jumlah sudut dalamnya 360o.
- Sisi-sisi yang berdekatan sama panjang.
- Perpotongan kedua diagonalnya membentuk sudut 90o atau saling tegak lurus.
- Salah satu diagonal dibagi menjadi dua sama panjang oleh diagonal yang lain.
g. Lingkaran, adalah bidang datar yang terbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik asal dengan jarak yang sama. Jarak tersebut biasanya dinamakan r, atau radius, atau jari-jari.
E. Kedudukan Titik, Garis, dan Bidang
1. Kedudukan titik terhadap garis
Ada dua kedudukan titik terhadap garis, yaitu:
- Titik terletak pada garis (titik A).
- Titik terletak di luar garis (titik B).
2. Kedudukan titik terhadap bidang
Ada dua kemungkinan kedudukan titik terhadap bidang, yaitu:
- Titik terletak pada bidang (α) {A, B, C, D}.
- Titik terletak di luar bidang (α) {E, F}.
3. Kedudukan antara dua garis
Ada 4 kemungkinan kedudukan antara dua garis, yaitu:
- Saling berimpit, dua buah garis dikatakan saling berimpit apabila kedua garis itu sama.Misal garis AB berimpit dengan AB.
- Saling berpotongan, dua buah garis dikatakan saling berpotongan apabila kedua garis itu mempunyai hanya satu titik persekutuan.Jika dua buah garis berpotongan, maka kedua garis itu terletak pada satu bidang.
- Sejajar, dua buah garis dikatakan sejajar jika kedua garis tersebut terletak pada satu bidang dan tidak mempunyai titik persekutuan.
- Saling bersilangan, dua buah garis dikatakan saling bersilangan apabila kedua garis itu tidak sebidang.
4. Kedudukan garis terhadap bidang, Ada tiga kemungkinan kedudukan garis terhadap bidang garis sejajar dengan bidang, garis berpotongan dengan bidang, atau garis terletak pada bidang.
artikel ini disalin lengkap dari: http://www.apyusa.com/2015/10/geometri-bidang-titik-garis-sudut-bidang.html#
halaman utama website: http://www.apyusa.com/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
A. Titik
Secara matematik definisi titik adalah sesuatu yang tidak mempunyai bagian sama sekali, tidak berbentuk dan tidak mempunyai ukuran.
Dari pengertian di atas, maka titik dapat dijabarkan sebagai berikut:
1. Tidak mempunyai ukuran
2. Tidak memeiliki panjang, lebar atua tebal.
3. Memiliki tempat (posisi)
4. Tidak dapat dilihat
Titik adalah bagian terkecil dari suatu objek geometri, yang menempati suatu tempat, yang tidak memiliki panjang, lebar, dan tinggi.Titik adalah suatu idea, benda pikiran yang bersifat abstrak. Dikarenakan titik tidak bisa dijelaskan dengan cara biasa, Titik termasuk sesuatu yang tak terdefinisi.
Berdasarkan penjabaran di atas, maka untuk menandai sebuah titik dapat disimbolkan dalam wujud noktah atau silang:
1. “.” Noktah untuk mewujudkan titik.
2. “x” Silang untuk mewujudkan titik.
Ingat! Nama sebuah titik menggunakan huruf kapital. Contohnya: A
B. Garis
Garis adalah himpunan dari titik-titik yang mempunyai panjang tak terhingga tetapi tidak memiliki lebar atau tebal.Panjangnya tak terbatas, lurus, tidak mempunyai ketebalan, dan tidak mempunyai ujung.
Gambar diatas untuk menunjukkan sebuah garis, dan penjelasannya sebagai berikut:
Melalui dua buah titik A dan B dapat digambar sebuah garis AB dan ditulis AB. Karena sifatnya tidak terbatas atau tidak terhingga, maka gambar (model) garis diberi panah pada kedua ujungnya.
Ciri-ciri garis yaitu:
1. Tidak mempunyai pangkal.
2. Tidak mempunyai ujung.
3. Panjangnya tak terhingga.
Titik yang terletak pada satu garis yang sama disebut titik-titik segaris (kolinear). Misalnya titik-titik A dan B yang terletak pada satu garis:
Dua garis disebut sejajar, jika keduanya tidak saling berpotongan atau berimpit. Jadi dapat dikatakan bahwa satu garis adalah sejajar dengan dirinya sendiri.
Tiga atau lebih garis yang melalui satu titik yang sama disebut garis setitik atau garis yang kongruen.
Ruas garis digambarkan diatas penjelasanya sebagai berikut:
Disebut ruas garis AB ditulis AB (tidak dengan panah). Ruas garis AB adalah himpunan titik-titik A dan B dan semua titik-titik diantara A dan B. Ciri-ciri ruas garis yaitu:
1. Mempunyai pangkal.
2. Mempunyai ujung.
3. Panjangnya terhingga (terbatas/dapat diukur).
Sinar garis digambarkan diatas, penjelasannya sebagai berikut:
Disebut sinar garis AB ditulis AB .Sinar AB adalah himpunan bagian dari garis termasuk titik A dan semua titik di sisi/ di pihak yang sama. Ciri-ciri sinar garis yaitu:
1. Mempunyai pangkal.
2. Tidak mempunyai ujung (digambar panah).
3. Panjangnya tidak terhingga.
C. Sudut
Sudut dibentuk oleh dua garis lurus yang berpotongan pada satu titik yang sisi-sisinya bersekutu pada salah satu ujungnya. Ciri-cirinya yaitu sisi-sisi sudut dibentuk oleh ruas-ruas garis dan sudut terbentuk karena ruas-ruas garis yang pangkalnya bersekutu (bertemu) pada satu titik yang disebut titik sudut.
Berdasarkan besar sudutnya, maka sudut digolongkan menjadi empat jenis, yaitu:
1. Sudut lurus adalah sudut yang besarnya 180o.
2. Sudut siku adalah sudut yang besarnya 90o.
3. Sudut lancip adalah sudut yang besarnya antara 0o – 90o.
4. Sudut tumpul adalah sudut yang besarnya lebih dari 90o.
D. Bidang
Bidang adalah permukaan rata yang meluas ke segala arah,tak terbatas, terus-menerus dalam semua arah, dan tidak memiliki ketebalan.Bidang adalah himpunan titik-titik yang memiliki luas tak terhingga.Bidang terdiri dari bidang datar dan bidang ruang.
Bidang datar disebut juga bidang berdimensi dua karena hanya mengandung unsur panjang dan lebar.Berikut ini merupakan macam-macam bidang datar, yaitu:
1. Segitiga
Segitiga adalah gabungan dari tiga segmen/ruas garis yang titik-titiknya tidak kolinier (tidak terletak pada satu garis). Ditinjau dari besar sudutnya, segitiga digolongkan menjadi:
a. Segitiga lancip (ketiga sudutnya lancip).
b. Segitiga siku-siku (salah satu sudutnya 90o).
c. Segitiga tumpul (salah satu sudutnya tumpul, >90o).
Sedangkan ditinjau dari panjang sisinya, segitiga digolongkan menjadi:
a. Segitiga sama sisi yang ketiga sisinya sama panjang.
b. Segitiga sama kaki yang mempunyai dua sisi yang sama panjang.
c. Segitiga sembarang yang ketiga sisinya tidak sama panjang.
Secara umum, sifat-sifat segitiga adalah sebagai berikut:
a. Mempunyai tiga sisi yang ketiga ujungnya saling bertemu dan membentuk tiga sudut.
b. Mempunyai tiga buah titik sudut.
c. Ketiga sudut besarnya 180o.
2. Segi Empat
Segi empat adalah suatu bangun yang mempunyai 4 sisi dan 4 sudut. Segi empat digolongkan menjadi:
a. Persegi (bujur sangkar), adalah bidang datar yang semua sisinya sama panjang dan keempat sudutnya siku-siku.
Sifat-sifat persegi yaitu:
- Jumlah sudut dalamnya 360o.
- Keempat sudutnya siku-siku.
- Sisi-sisinya sama panjang.
- Diagonalnya sama panjang.
- Perpotongan diagonalnya membentuk sudut 90o atau saling tegak lurus.
- Tiap-tiap sudut dibagi oleh diagonal menjadi dua bagian sama besar.
b. Persegi panjang, adalah segi empat yang keempat sudutnya siku-siku danmempunyai sisi berhadapan yang sama panjang. Sifat-sifat persegi panjang yaitu:
- Setiap sudutnya siku-siku.
- Sisi-sisi yang berhadapan sama panjang.
- Jumlah sudut dalamnya 360o.
- Kedua diagonalnya berpotongan di tengah.
c. Jajar genjang, adalah bidang datar bersegi empat, sisi-sisi yang berhadapan sama panjang dan sejajar. Sifat-sifat jajar genjang yaitu:
- Jumlah sudut dalamnya 360o.
- Sudut-sudut yang berhadapan sama besar.
- Sisi-sisi yang berhadapan sama panjang.
- Diagonal yang satu membagi diagonal yang lain menjadi dua bagian yang sama panjang.
d. Belah ketupat, dapat disebut juga jajar genjang yang keempat sisinya sama panjang. Sifat-sifat belah ketupat yaitu:
- Jumlah sudut dalamnya 360o.
- Sudut-sudut yang berhadapan sama besar.
- Sisi-sisinya sama panjang.
- Diagonalnya saling berpotongan dan saling tegak lurus (membentuk sudut 90o).
- Tiap-tiap sudut dibagi oleh diagonal menjadi dua sama besar.
e. Trapesium, adalah segi empat yang dua sisinya sejajar. Ada 3 jenis trapesium, yaitu trapesium yang keempat sisinya tidak sama panjang, trapesium sama kaki yang kedua sisi tegaknya sama panjang, dan trapesium siku-siku yang salah satu sudutnya siku-siku. Salah satu sifat trapesium yaitu dua sisinya sejajar.
f. Layang-layang, adalah segi empat yang kedua pasang sisinya saling berdekatan sama panjang dan salah satu diagonalnya memotong tegak lurus sumbu diagonal lainnya. Sifat-sifatnya yaitu:
- Jumlah sudut dalamnya 360o.
- Sisi-sisi yang berdekatan sama panjang.
- Perpotongan kedua diagonalnya membentuk sudut 90o atau saling tegak lurus.
- Salah satu diagonal dibagi menjadi dua sama panjang oleh diagonal yang lain.
g. Lingkaran, adalah bidang datar yang terbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik asal dengan jarak yang sama. Jarak tersebut biasanya dinamakan r, atau radius, atau jari-jari.
E. Kedudukan Titik, Garis, dan Bidang
1. Kedudukan titik terhadap garis
Ada dua kedudukan titik terhadap garis, yaitu:
- Titik terletak pada garis (titik A).
- Titik terletak di luar garis (titik B).
2. Kedudukan titik terhadap bidang
Ada dua kemungkinan kedudukan titik terhadap bidang, yaitu:
- Titik terletak pada bidang (α) {A, B, C, D}.
- Titik terletak di luar bidang (α) {E, F}.
3. Kedudukan antara dua garis
Ada 4 kemungkinan kedudukan antara dua garis, yaitu:
- Saling berimpit, dua buah garis dikatakan saling berimpit apabila kedua garis itu sama.Misal garis AB berimpit dengan AB.
- Saling berpotongan, dua buah garis dikatakan saling berpotongan apabila kedua garis itu mempunyai hanya satu titik persekutuan.Jika dua buah garis berpotongan, maka kedua garis itu terletak pada satu bidang.
- Sejajar, dua buah garis dikatakan sejajar jika kedua garis tersebut terletak pada satu bidang dan tidak mempunyai titik persekutuan.
- Saling bersilangan, dua buah garis dikatakan saling bersilangan apabila kedua garis itu tidak sebidang.
4. Kedudukan garis terhadap bidang, Ada tiga kemungkinan kedudukan garis terhadap bidang garis sejajar dengan bidang, garis berpotongan dengan bidang, atau garis terletak pada bidang.
artikel ini disalin lengkap dari: http://www.apyusa.com/2015/10/geometri-bidang-titik-garis-sudut-bidang.html#
halaman utama website: http://www.apyusa.com/
jika mencari artikel yang lebih menarik lagi, kunjungi halaman utama website tersebut. Terimakasih!
No comments:
Post a Comment